Page 129 - Linear Algebra Done Right

Chapter 6. Inner-Product Spaces
116
1
0.5
-3 -2 -1 1 2 3

-0.5

-1
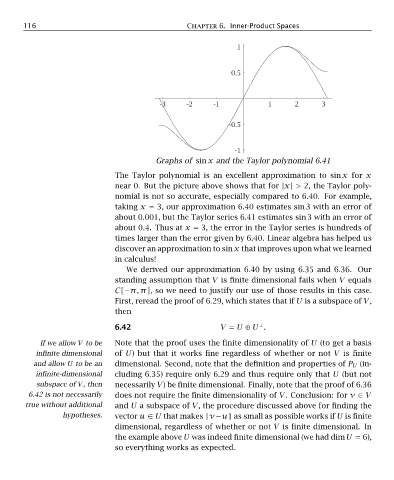
Graphs of sin x and the Taylor polynomial 6.41
The Taylor polynomial is an excellent approximation to sin x for x
near 0. But the picture above shows that for |x| > 2, the Taylor poly-
nomial is not so accurate, especially compared to 6.40. For example,
taking x = 3, our approximation 6.40 estimates sin 3 with an error of
about 0.001, but the Taylor series 6.41 estimates sin 3 with an error of
about 0.4. Thus at x = 3, the error in the Taylor series is hundreds of
times larger than the error given by 6.40. Linear algebra has helped us
discover an approximation to sin x that improves upon what we learned
in calculus!
We derived our approximation 6.40 by using 6.35 and 6.36. Our
standing assumption that V is finite dimensional fails when V equals
C[−π, π], so we need to justify our use of those results in this case.
First, reread the proof of 6.29, which states that if U is a subspace of V,
then
6.42 V = U ⊕ U .
⊥
If we allow V to be Note that the proof uses the finite dimensionality of U (to get a basis
infinite dimensional of U) but that it works fine regardless of whether or not V is finite
and allow U to be an dimensional. Second, note that the definition and properties of P U (in-
infinite-dimensional cluding 6.35) require only 6.29 and thus require only that U (but not
subspace of V, then necessarily V) be finite dimensional. Finally, note that the proof of 6.36
6.42 is not necessarily does not require the finite dimensionality of V. Conclusion: for v ∈ V
true without additional and U a subspace of V, the procedure discussed above for finding the
hypotheses. vector u ∈ U that makes v−u as small as possible works if U is finite
dimensional, regardless of whether or not V is finite dimensional. In
the example above U was indeed finite dimensional (we had dim U = 6),
so everything works as expected.