Page 20 - Linear Algebra Done Right

Chapter 1. Vector Spaces
6
We let 0 denote the list of length n all of whose coordinates are 0:
0 = (0,..., 0).
Note that we are using the symbol 0 in two different ways—on the
left side of the equation above, 0 denotes a list of length n, whereas
on the right side, each 0 denotes a number. This potentially confusing
practice actually causes no problems because the context always makes
clear what is intended. For example, consider the statement that 0 is
n
an additive identity for F :
x + 0 = x

n
for all x ∈ F . Here 0 must be a list because we have not defined the
n
sum of an element of F (namely, x) and the number 0.
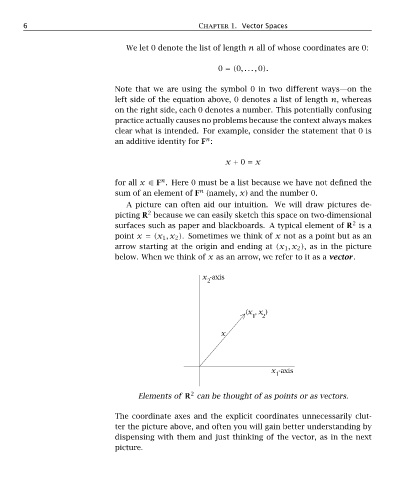
A picture can often aid our intuition. We will draw pictures de-
2
picting R because we can easily sketch this space on two-dimensional
2
surfaces such as paper and blackboards. A typical element of R is a
point x = (x 1 ,x 2 ). Sometimes we think of x not as a point but as an
arrow starting at the origin and ending at (x 1 ,x 2 ), as in the picture
below. When we think of x as an arrow, we refer to it as a vector.

x -axis
2

(x , x )
1 2
x

x -axis
1

2
Elements of R can be thought of as points or as vectors.
The coordinate axes and the explicit coordinates unnecessarily clut-
ter the picture above, and often you will gain better understanding by
dispensing with them and just thinking of the vector, as in the next
picture.