Page 195 - MATLAB Recipes for Earth Sciences

190 7 Spatial Data

Kriging Estimate Kriging Variance
1 200

0.9 180
0.8 160
0.7 140
y−coordinates 0.6 y−coordinates 120

0.5
100
0.4
60
0.3 80
0.2 40

0.1 20
0 0
0 0.2 0.4 0.6 0.8 1 0 50 100 150 200
x−coordinates x−coordinates

10 20 30 40 50 60 10 20 30 40 50 60
a b

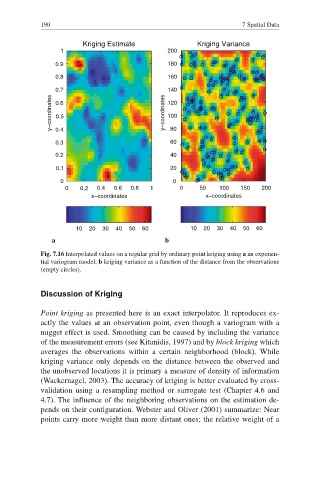
Fig. 7.16 Interpolated values on a regular grid by ordinary point kriging using a an exponen-
tial variogram model; b kriging variance as a function of the distance from the observations
(empty circles).

Discussion of Kriging

Point kriging as presented here is an exact interpolator. It reproduces ex-
actly the values at an observation point, even though a variogram with a
nugget effect is used. Smoothing can be caused by including the variance
of the measurement errors (see Kitanidis, 1997) and by block kriging which
averages the observations within a certain neighborhood (block). While
kriging variance only depends on the distance between the observed and
the unobserved locations it is primary a measure of density of information
(Wackernagel, 2003). The accuracy of kriging is better evaluated by cross-
validation using a resampling method or surrogate test (Chapter 4.6 and
4.7). The influence of the neighboring observations on the estimation de-

pends on their configuration. Webster and Oliver (2001) summarize: Near

points carry more weight than more distant ones; the relative weight of a