Page 54 - Mechanical Behavior of Materials

Section 2.4 Elastic Deformation and Theoretical Strength 53

5
10
Polystyrene
4
10
Glassy
3
10
MPa 10 2
Modulus, 10 T g Leathery

Elastic 1 Rubbery

E, 10 -1 Rubbery flow
-2
10
-3 Liquid
10
T m
-4
10
60 80 100 120 140 160 180 200
o
Temperature, C
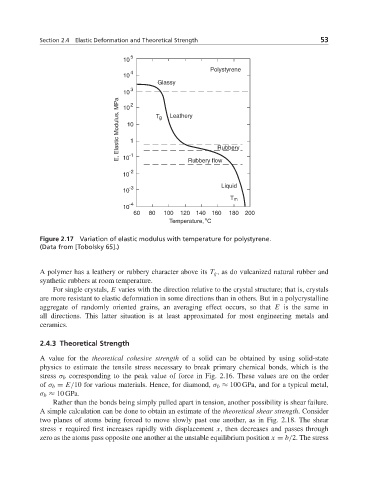
Figure 2.17 Variation of elastic modulus with temperature for polystyrene.
(Data from [Tobolsky 65].)

A polymer has a leathery or rubbery character above its T g , as do vulcanized natural rubber and
synthetic rubbers at room temperature.
For single crystals, E varies with the direction relative to the crystal structure; that is, crystals
are more resistant to elastic deformation in some directions than in others. But in a polycrystalline
aggregate of randomly oriented grains, an averaging effect occurs, so that E is the same in
all directions. This latter situation is at least approximated for most engineering metals and
ceramics.

2.4.3 Theoretical Strength

A value for the theoretical cohesive strength of a solid can be obtained by using solid-state
physics to estimate the tensile stress necessary to break primary chemical bonds, which is the
stress σ b corresponding to the peak value of force in Fig. 2.16. These values are on the order
of σ b = E/10 for various materials. Hence, for diamond, σ b ≈ 100 GPa, and for a typical metal,
σ b ≈ 10 GPa.
Rather than the bonds being simply pulled apart in tension, another possibility is shear failure.
A simple calculation can be done to obtain an estimate of the theoretical shear strength. Consider
two planes of atoms being forced to move slowly past one another, as in Fig. 2.18. The shear
stress τ required first increases rapidly with displacement x, then decreases and passes through
zero as the atoms pass opposite one another at the unstable equilibrium position x = b/2. The stress