Page 177 - Mechanical Engineers' Handbook (Volume 4)

166 Heat-Transfer Fundamentals

4
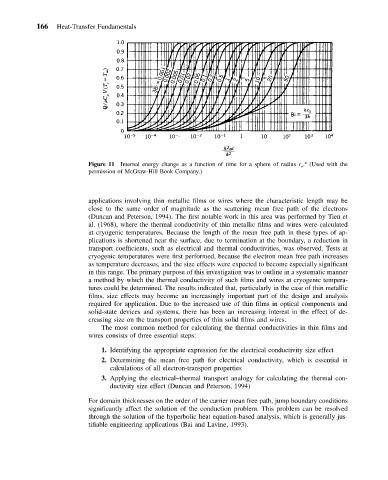
Figure 11 Internal energy change as a function of time for a sphere of radius r o . (Used with the
permission of McGraw-Hill Book Company.)

applications involving thin metallic films or wires where the characteristic length may be
close to the same order of magnitude as the scattering mean free path of the electrons
(Duncan and Peterson, 1994). The first notable work in this area was performed by Tien et
al. (1968), where the thermal conductivity of thin metallic films and wires were calculated
at cryogenic temperatures. Because the length of the mean free path in these types of ap-
plications is shortened near the surface, due to termination at the boundary, a reduction in
transport coefficients, such as electrical and thermal conductivities, was observed. Tests at
cryogenic temperatures were first performed, because the electron mean free path increases
as temperature decreases, and the size effects were expected to become especially significant
in this range. The primary purpose of this investigation was to outline in a systematic manner
a method by which the thermal conductivity of such films and wires at cryogenic tempera-
tures could be determined. The results indicated that, particularly in the case of thin metallic
films, size effects may become an increasingly important part of the design and analysis
required for application. Due to the increased use of thin films in optical components and
solid-state devices and systems, there has been an increasing interest in the effect of de-
creasing size on the transport properties of thin solid films and wires.
The most common method for calculating the thermal conductivities in thin films and
wires consists of three essential steps:
1. Identifying the appropriate expression for the electrical conductivity size effect
2. Determining the mean free path for electrical conductivity, which is essential in
calculations of all electron-transport properties
3. Applying the electrical–thermal transport analogy for calculating the thermal con-
ductivity size effect (Duncan and Peterson, 1994)

For domain thicknesses on the order of the carrier mean free path, jump boundary conditions
significantly affect the solution of the conduction problem. This problem can be resolved
through the solution of the hyperbolic heat equation-based analysis, which is generally jus-
tifiable engineering applications (Bai and Lavine, 1993).