Page 243 - MODELING OF ASPHALT CONCRETE

Unified Disturbed State Constitutive Modeling of Asphalt Concr ete 221

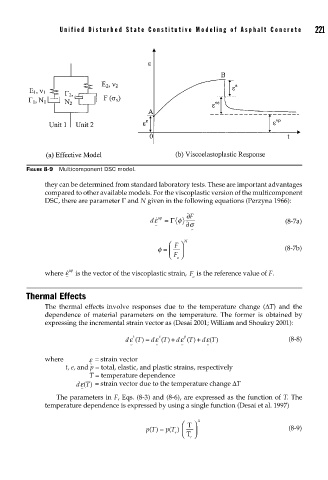
FIGURE 8-9 Multicomponent DSC model.

they can be determined from standard laboratory tests. These are important advantages
compared to other available models. For the viscoplastic version of the multicomponent
DSC, there are parameter Γ and N given in the following equations (Perzyna 1966):
∂ F
d ε up = Γ φ ∂ σ (8-7a)
~
~
⎛ F ⎞ N
φ = ⎜ ⎟ (8-7b)
⎝ F o ⎠
up
where ε is the vector of the viscoplastic strain, F is the reference value of F.
~ o
Thermal Effects
The thermal effects involve responses due to the temperature change (ΔT) and the
dependence of material parameters on the temperature. The former is obtained by
expressing the incremental strain vector as (Desai 2001; William and Shoukry 2001):

t
e
p
dε () = dε () + dε () + d T (8-8)
T
T
ε()
T
~ ~ ~ ~
where ε = strain vector
~
t, e, and p = total, elastic, and plastic strains, respectively
T = temperature dependence
dT = strain vector due to the temperature change ΔT
ε()
~
The parameters in F, Eqs. (8-3) and (8-6), are expressed as the function of T. The
temperature dependence is expressed by using a single function (Desai et al. 1997)
pT() = pT ) ⎛ T ⎞ ⎟ λ (8-9)
(
r ⎜
⎝ T r ⎠