Page 77 - Modern physical chemistry

66 The First Law for Energy

4.4 The First Law

By no macroscopic process can energy be created or destroyed. Only transforma-
tions of energy occur. This limitation is embodied in thefirst law of thermodynamics:
The amount of energy required to take a system from one state to another is indepen-
dent of how the system goes between the two states.
The internal energy E of a given system depends only on the state of the system. This
is altered by the heat transferred to the system and the work done on it. For an infinites-
imal change in a system, we have
dE=dq+dw. [4.12]
Integrating this from state 1 to state 2 yields

[4.13]
where q is the heat absorbed in the process and w the work done on the system in the
process.
A given change in the system may be effected by various q's and w's. A person cannot
say that a given system has a particular heat content q or a particular work content w.
However, there are constraints on the q's and w's needed to cause certain changes.
By experiment, a pure uniform substance cannot have its temperature lowered at a given
pressure without removing heat. But this involves the second law of thermodynamics,
which will be considered later.
Since q and w are not functions of state, the differentials dq and dw are not exact.
Their integrals depend on how the system is taken from the initial state to the final state.

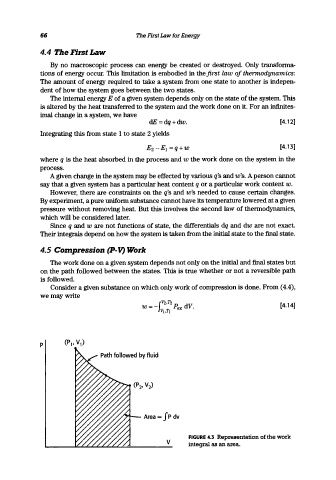
4.5 Compression (P-V) Work
The work done on a given system depends not only on the initial and final states but
on the path followed between the states. This is true whether or not a reversible path
is followed.
Consider a given substance on which only work of compression is done. From (4.4),
we may write
[4.14]

P
Path followed by fluid

Area = Ip dv

v FIGURE 4.3 Representation of the work
integral as an area.