Page 137 - Numerical Analysis and Modelling in Geomechanics

118 C.W.W.NG AND Q.SHI

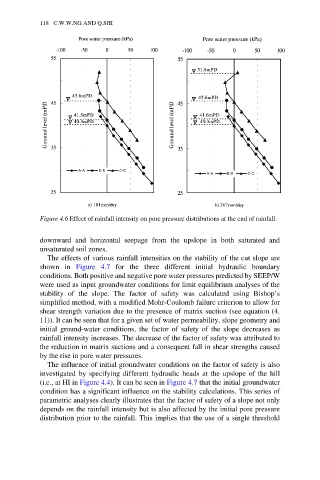
Figure 4.6 Effect of rainfall intensity on pore pressure distributions at the end of rainfall.

downward and horizontal seepage from the upslope in both saturated and
unsaturated soil zones.
The effects of various rainfall intensities on the stability of the cut slope are
shown in Figure 4.7 for the three different initial hydraulic boundary
conditions. Both positive and negative pore water pressures predicted by SEEP/W
were used as input groundwater conditions for limit equilibrium analyses of the
stability of the slope. The factor of safety was calculated using Bishop’s
simplified method, with a modified Mohr-Coulomb failure criterion to allow for
shear strength variation due to the presence of matrix suction (see equation (4.
11)). It can be seen that for a given set of water permeability, slope geometry and
initial ground-water conditions, the factor of safety of the slope decreases as
rainfall intensity increases. The decrease of the factor of safety was attributed to
the reduction in matrix suctions and a consequent fall in shear strengths caused
by the rise in pore water pressures.
The influence of initial groundwater conditions on the factor of safety is also
investigated by specifying different hydraulic heads at the upslope of the hill
(i.e., at HI in Figure 4.4). It can be seen in Figure 4.7 that the initial groundwater
condition has a significant influence on the stability calculations. This series of
parametric analyses clearly illustrates that the factor of safety of a slope not only
depends on the rainfall intensity but is also affected by the initial pore pressure
distribution prior to the rainfall. This implies that the use of a single threshold