Page 97 - Numerical Methods for Chemical Engineering

86 2 Nonlinear algebraic systems

1

1
viscsit in a s 1

1 2
1 −1 1 1 1 1 2
sear r ate in s −1
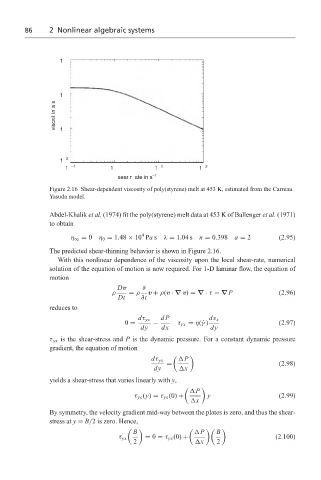
Figure 2.16 Shear-dependent viscosity of poly(styrene) melt at 453 K, estimated from the Carreau–
Yasuda model.

Abdel-Khalik et al. (1974) fit the poly(styrene) melt data at 453 K of Ballenger et al. (1971)
to obtain
4
η ∞ = 0 η 0 = 1.48 × 10 Pa s λ = 1.04 s n = 0.398 a = 2 (2.95)
The predicted shear-thinning behavior is shown in Figure 2.16.
With this nonlinear dependence of the viscosity upon the local shear-rate, numerical
solution of the equation of motion is now required. For 1-D laminar flow, the equation of
motion
Dv ∂
ρ = ρ v + ρ(v · ∇ v) = ∇ · τ − ∇P (2.96)
Dt ∂t
reduces to
dτ yx dP dv x
0 = − τ yx = η(˙γ ) (2.97)
dy dx dy
τ yx is the shear-stress and P is the dynamic pressure. For a constant dynamic pressure
gradient, the equation of motion

dτ yx P
= (2.98)
dy x
yields a shear-stress that varies linearly with y,
P

τ yx (y) = τ yx (0) + y (2.99)
x
By symmetry, the velocity gradient mid-way between the plates is zero, and thus the shear-
stress at y = B/2 is zero. Hence,
B P B

τ yx = 0 = τ yx (0) + (2.100)
2 x 2