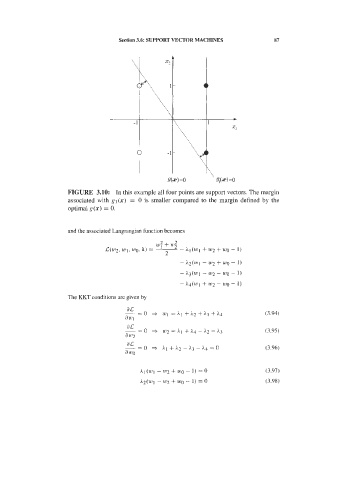
Page 104 -

4.2 Bayesian Classification 9 1

Assume now that we were allowed to measure the feature vector x of the
presented cork stopper. Let P(w, ( x) be the conditional probability of the cork
stopper represented by x belonging to class q. If we are able to determine the
probabilities P(wl 1 x) and P(w2 I x) , the sensible decision is now:

If P(w, I x) > P(w2 I x) we decide x E w, ;
If P(w , I x) < P(w2 I x) we decide x E w2 ;
If P(w, I x) = P(w2 I x) the decision is arbitrary.

We can condense (4-13) as:

If P(w,(x) > P(w,(x) then x~w, else x~w,. (4-13a)

The posterior probabilities P(wi ( x) can be computed if we know the pdfs of
the distributions of the feature vectors in both classes. We then calculate the
respective p(x 1 a;), the so-called likelihood of x. As a matter of fact, the well-
known Bayes law states that:

C
with p(x) = p(x I wi)P(wj) , the total probability of x.
i=l

Note that P(wi) and P(wi I x) are discrete probabilities (symbolized by capital
letter), whereas p(x lai) and p(x) are values of pdf functions. Note also that the
term p(x) is a common term in the comparison expressed by (4- 13a), therefore we
may rewrite for two classes:

or,

if v(x) = p(x I o1 ) >- P(w2 ) then xc w, else xc w,
P(X l w2 ) P(w, )

In the formula (4-15a), v(x) is the so-called likelihood ratio. The decision
depends on how this ratio compares with the inverse prevalence ratio or prevalence
threshold, P(@)IP(wl).
Let us assume for the cork stoppers problem that we only used feature N, x=[N],
and that a cork was presented with x=[65].
Figure 4.12 shows the histograms of both classes with superimposed normal
curve.