Page 46 -

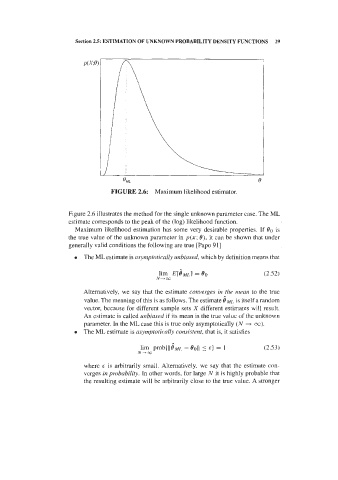
32 2 Pattern Discrimination

Figure 2.11. Linear transformation of a circular pattern cluster into an elliptic one.
The dots represent feature vectors.

We see that this linear transformation amounts to a scaling operation (e.g. x, is
stretched by a factor of 2) concomitant with a translation effect of the mean due to
a,, and all, plus a mirroring efect due to a12 and all. If the matrix A is anti-
symmetric with all = - all, a rotation eflect is observed instead (see Exercise 2.7).
[ : : ; I = [:I.
The transformed mean is:

We see that the cluster structure changed from circular to ellipsoidal equidistant
surfaces, whose shape is dependent on the particular matrix A, i.e., in the
transformed space similar patterns have feature vectors lying on the same ellipsis.
The generalization to any d-dimensional space is straightforward: the equidistant
surfaces in the transformed space for the y vectors are hyperell@oids, whose
distance from the prototype is given by the Mahalanobis metric (in a broad sense):

Notice that for A=I, unity matrix, one obtains the Euclidian metric as a
particular case of the Mahalanobis metric. In order for formula (2-13) to represent
a distance, matrix A must be such that p(y) > 0 for all y # 0. A is then called a
positive definite matrix and p(y) a positive definite form of matrix A, known as a
quadratic form. For d=2 the quadratic form is:

Notice that with hyperellipsoidal equidistant surfaces one can obtain decision
surfaces that are either linear or quadratic as shown in Figure 2.12.