Page 89 -

76 3 Data Clusterine

where P(A) is the proportion of times the k judges agree and P(E) is the proportion
of times that we would expect the k judges to agree by chance. If there is complete
agreement among the judges, then el (P(A)=l, P(E)=O). If there is no agreement
among the judges other than what would be expected by chance, then GO
(P(A)=P(E)). The values of P(A) and P(E) are computed as follows:

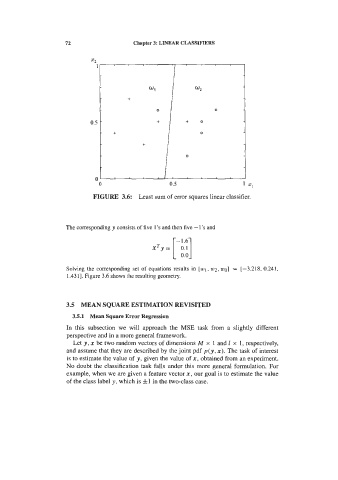
For the Rocks example these quantities are computed as P(A)=0.971 and
P(E)=0.418, resulting in a high value of K, ~=0.95. In order to test the significance
of K, the following statistic, approximately normally distributed for large n with
zero mean and unit standard deviation, is used:

The value of z = 9.5 is obtained for the present example, allowing us to conclude
significantly high agreement at a a= 0.01 significance level (zeo.ol = 2.32).

Bibliography

Andrews HC (1972) Introduction to Mathematical Techniques in Pattern Recognition. John
Wiley & Sons, Inc.
Barnett S (1979) Matrix Methods for Engineers and Scientists. McGraw Hill Book Co.
Borg I, Groenen P (1997) Modern Multidimensional Scaling. Springer-Verlag.
Chambers JM, Kleiner B (1982) Graphical Techniques for Multivariate Data and for
Clustering. In: Krishnaiah PR, Kanal LN (eds), Handbook of Statistics vo1.2, North
Holland Pub. Co., 209-244.
Chien, Yi Tzuu (1978) Interactive Pattcrn Recognition. Marcel Dekker Inc.
De Leeuw J, Heiser W (1982) Theory of Multidimensional Scaling. In: Krishnaiah PR,
Kanal LN (eds), Handbook of Statistics vo1.2, North Holland Pub. Co., 285-316.
Duda R, Hart P (1973) Pattern Classification and Scene Analysis. Wiley, New York.
Gordon A (1996) Hierarchical Classification. In: Arabie P, Hubert LJ, De Soete G (eds)
Clustering and Classification. World Scientific Pub. Co., Singapore.
Hartigan JA (1975) Clustering Algorithms. John Wiley & Sons, New York.
Kaufman L, Rousseeuw PJ (1990) Finding Groups in Data. An Introduction to Cluster
Analysis. John Wiley & Sons, Inc.