Page 95 -

82 4 Statistical Classification

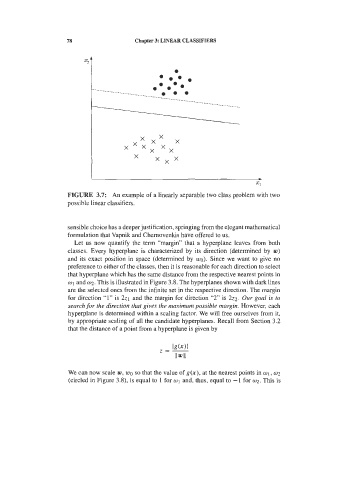
Counting the number of training set cases wrongly classified, it is observed that
the overall error falls to 18%. The addition of PRTlO seems beneficial.
In general, the minimum distance classifier (using any distance metric) has the
structure represented in Figure 4.4, where x is the input feature vector to be
assigned to one of c classes wk(k=l, . . ., c) represented by the respective prototypes
mk-

Select Class
the
minimum

Figure 4.4. Minimum distance classifier system for a feature vector x as input.

4.1.2 Euclidian Linear Discriminants

The previous minimum distance classifier for two classes and a two-dimensional
feature vector, using a Euclidian metric, has a straightforward generalization
(Figure 4.4) for any d-dimensional feature vector x and any number of classes, ~k
(k=l, ..., c), represented by their prototypes mk. The square of the Euclidian
distance between a feature vector x and a prototype mk is expressed as follows:

We choose class 4, therefore the mk, which minimizes d;(x). Grouping
together the terms dependent on mk, we obtain:

Let us assume c=2. The decision boundary between the classes corresponds to:

d: (x) = di (x) . (4-3b)

Thus, using (4-3a):