Page 154 - Percolation Models for Transport in Porous Media With

150 CHAPTER 8. CONDUCTIVITY AND ELECTRIC CURRENT

a

lg£.

1,0
fJ,J tgl I I,
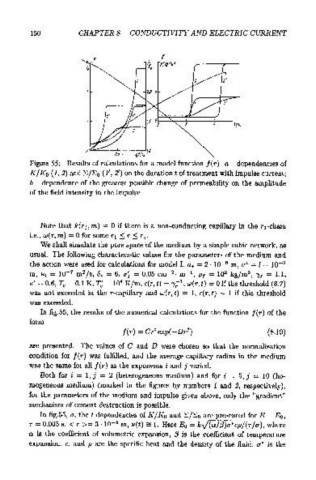
Figure 55: Results of calculations for a model function f(r): a- dependencies of
K/Ko (1, 2) and "£/"£0 (1', 2') on the duration t of treatment with impulse current;
b- dependence of the greatest possible change of permeability on the amplitude
of the field intensity in the impulse

Note that k(r 1 ,m) = 0 if there is a non-conducting capillary in the r1-chain
i.e., w(r,m) = 0 for some r1 ~ r ~ rz.
We shall simulate the pore space of the medium by a simple cubic network, as
usual. The following characteristic values for the parameters of the medium and
the action were used for calculations for model I. a* = 2. w- 6 m, a* = l = w- 3
m, Kt = 10- 7 m 2 /s, b. = 6, <T~ = 0.05 cm- · m- ' P! = 10 kg/m , 'Ycr = 1.1,
1
3
3
2
K' = 0.6, Tc = 0.1 K, T: = 10 4 Kfm, f(r, t) = "'(; 1 , w(r, t) = 0 if the threshold (8.7)
was not exceeded in the r-capillary and w(r, t) = 1, f(r, t) = 1 if this threshold
was exceeded.
In fig.55, the results of the numerical calculations for the function J(r) of the
form
f(r) = Cri exp( -Dri) (8.19)
are presented. The values of C and D were chosen so that the normalization
condition for f(r) was fulfilled, and the average capillary radius in the medium
was the same for all f(r) as the exponents i and j varied.
Both for i = 1, j = 2 (heterogeneous medium) and for i = 5, j = 10 (ho-
mogeneous medium) (marked in the figures by numbers 1 and 2, respectively),
for the parameters of the medium and impulse given above, only the "gradient"
mechanism of cement destruction is possible.
In fig.55, a, the t dependencies of K/Ko and "E./"£0 are presented forE= E0 ,
r = 0.005 s, < r >= 3 ·10- 4 m, u(t) 9! 1. Here Eo= kJ(o:/fJ)o-*cpf(rfo-), where
o: is the coefficient of volumetric expansion, f3 is the coefficient of temperature
expansion, c, and p are the specific heat and the density of the fluid, o-* is the