Page 361 - Petroleum Geology

331

I 141

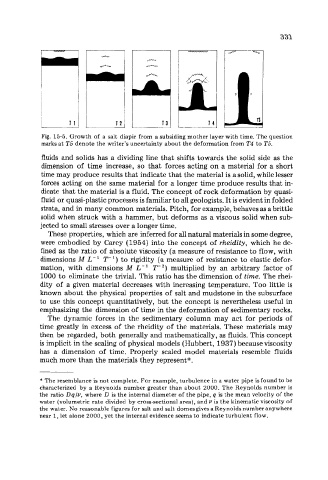
Fig. 15-5. Growth of a salt d pir from a subsiding mother layer with time. The question
marks at T5 denote the writer’s uncertainty about the deformation from T4 to T5.
fluids and solids has a dividing line that shifts towards the solid side as the
,.
. .,”
t ”
aimension 01 tune increase, so tnat Iorces actmg on a material lor a snort
<.
I.
” I-
.
1
time may produce results that indicate that the material is a solid, while lesser
forces acting on the same material for a longer time produce results that in-
dicate that the material is a fluid. The concept of rock deformation by quasi-
fluid or quasi-plastic processes is familiar to all geologists. It is evident in folded
strata, and in many common materials. Pitch, for example, behaves as a brittle
solid when struck with a hammer, but deforms as a viscous solid when sub-
jected to small stresses over a longer time.
These properties, which are inferred for all natural materials in some degree,
were embodied by Carey (1954) into the concept of rheidity, which he de-
fined as the ratio of absolute viscosity (a measure of resistance to flow, with
dimensions M L-’ T-’) to rigidity (a measure of resistance to elastic defor-
mation, with dimensions M L-’ T-2) multiplied by an arbitrary factor of
1000 to eliminate the trivial. This ratio has the dimension of time. The rhei-
dity of a given material decreases with increasing temperature. Too little is
known about the physical properties of salt and mudstone in the subsurface
to use this concept quantitatively, but the concept is nevertheless useful in
emphasizing the dimension of time in the deformation of sedimentary rocks.
The dynamic forces in the sedimentary column may act for periods of
time greatly in excess of the rheidity of the materials. These materials may
then be regarded, both generally and mathematically, as fluids. This concept
is implicit in the scaling of physical models (Hubbert, 1937) because viscosity
has a dimension of time. Properly scaled model materials resemble fluids
much more than the materials they represent*.

* The resemblance is not complete. For example, turbulence in a water pipe is found to be
characterized by a Reynolds number greater than about 2000. The Reynolds number is
the ratio Dq/v, where D is the internal diameter of the pipe, q is the mean velocity of the
water (volumetric rate divided by cross-sectional area), and v is the kinematic viscosity of
the water. No reasonable figures for salt and salt domesgivesa Reynolds number anywhere
near 1, let alone 2000, yet the internal evidence seems to indicate turbulent flow.