Page 107 - Petrology of Sedimentary Rocks

In general, immature rocks have very little original visible pore space, and little
chemical cement; submature (and higher) rocks have the pores either open or filled with
chemical cements like quartz or calcite.
2. Determine the sorting of the rock.

a. If it is not well sorted with a over 0.5$ (mm diameter ratio over 2.0), it
is SUBMATURE.

b. If it is well sorted with a under 0.54, go to (3).

The sorting borderline between submature and mature is depicted in the bottom figure
on the next page, which represents a set of spheres with a phi standard deviation of
exactly 0.5. Compare your sample with the figure to see if it is well enough sorted to
be mature.
3. Determine the roundness of quartz grains of sand size.

a. If the grains are subangular to very angular on Powers’ scale (p under
3.0, it is MATURE.

b. If the grains are subround to well rounded (p over 3.0) it is SUPER-
MATURE.

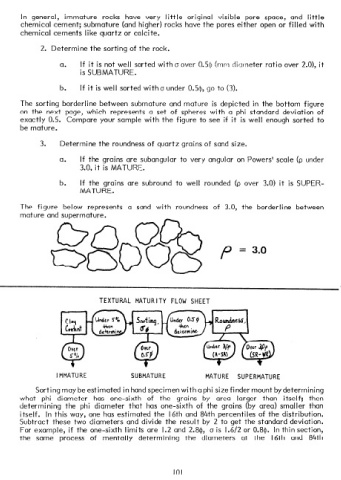
The figure below represents a sand with roundness of 3.0, the borderline between
mature and supermature.

TEXTURAL MATURITY FLOW SHEET

IMMATURE SUBMATURE MATURE SUPERMATURE

Sorting may be estimated in hand specimen with a phi size finder mount by determining
what phi diameter has one-sixth of the grains by area larger than itself; then
determining the phi diameter that has one-sixth of the grains (by area) smaller than
itself. In this way, one has estimated the 16th and 84th percentiles of the distribution.
Subtract these two diameters and divide the result by 2 to get the standard deviation.
For example, if the one-sixth limits are I .2 and 2.84, a is l.6/2 or 0.84. In thin section,
the same process of mentally determining the diameters at the 16th and 84th

IO1