Page 111 - Phase Space Optics Fundamentals and Applications

92 Chapter Three

is a useful tool for shift-variant pattern recognition. This operation
can be performed by a fractional Van der Lugt correlator, which is a
modification of the common one, where the first part is replaced by
the fractional FT system.
To maximize the Horner efficiency of the correlation operation,
phase-only filters are often used. It was shown in Ref. 57 that, in gen-
eral, the phase of the fractional FT for
= n with integer n contains
more information about the signal than the amplitude, and therefore,
the phase-only filters can also be applied in the fractional FT domains.
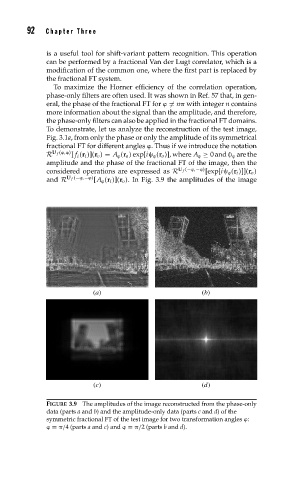
To demonstrate, let us analyze the reconstruction of the test image,
Fig. 3.1a, from only the phase or only the amplitude of its symmetrical
fractional FT for different angles
. Thus if we introduce the notation
U f (
,
)
R [ f i (r i )](r o ) = A
(r o ) exp[i
(r o )], where A
≥ 0 and
are the
amplitude and the phase of the fractional FT of the image, then the
U f (−
,−
)
considered operations are expressed as R [exp[i
(r i )]](r o )
U f (−
,−
)
and R [A
(r i )](r o ). In Fig. 3.9 the amplitudes of the image

(a) (b)

(c) (d)

FIGURE 3.9 The amplitudes of the image reconstructed from the phase-only
data (parts a and b) and the amplitude-only data (parts c and d) of the
symmetric fractional FT of the test image for two transformation angles
:

= /4 (parts a and c) and
= /2 (parts b and d).