Page 86 - Physical Principles of Sedimentary Basin Analysis

68 Linear elasticity and continuum mechanics

0 5000

4000
ζ* = ζ*(x)
2000
3000
z [m] 4000 ζ [m]
2000

6000
1000

8000 0
0 5000 10000 15000 20000 0 5000 10000 15000 20000
x [m] x [m]
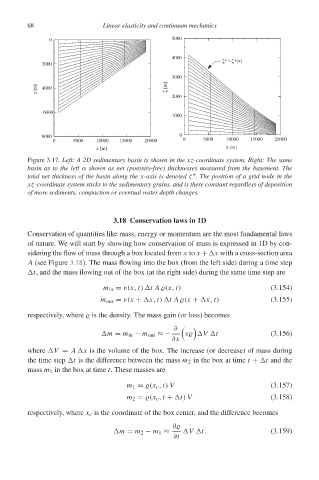
Figure 3.17. Left: A 2D sedimentary basin is shown in the xz-coordinate system. Right: The same
basin as to the left is shown as net (porosity-free) thicknesses measured from the basement. The
∗
total net thickness of the basin along the x-axis is denoted ζ . The position of a grid node in the
xζ-coordinate system sticks to the sedimentary grains, and is there constant regardless of deposition
of more sediments, compaction or eventual water depth changes.

3.18 Conservation laws in 1D
Conservation of quantities like mass, energy or momentum are the most fundamental laws
of nature. We will start by showing how conservation of mass is expressed in 1D by con-
sidering the flow of mass through a box located from x to x + x with a cross-section area
A (see Figure 3.18). The mass flowing into the box (from the left side) during a time step
t, and the mass flowing out of the box (at the right side) during the same time step are

m in = v(x, t) tA (x, t) (3.154)
m out = v(x + x, t) tA (x + x, t) (3.155)
respectively, where is the density. The mass gain (or loss) becomes
∂
m = m in − m out ≈− v V t (3.156)
∂x
where V = A x is the volume of the box. The increase (or decrease) of mass during
the time step t is the difference between the mass m 2 in the box at time t + t and the
mass m 1 in the box at time t. These masses are

m 1 = (x c , t) V (3.157)
m 2 = (x c , t + t) V (3.158)

respectively, where x c is the coordinate of the box center, and the difference becomes
∂
m = m 2 − m 1 ≈ V t. (3.159)
∂t