Page 62 - Physical chemistry eng

2.11 THE REVERSIBLE ADIABATIC EXPANSION AND COMPRESSION OF AN IDEAL GAS 39

We calculate ¢U = w from
-1
¢U = nC V,m (T - T ) = 2.5 mol * 12.47 J mol K -1 * (268 K - 325 K)
i
f
=-1.78 kJ
Because the temperature falls in the expansion, the internal energy and enthalpy decreases:
¢H =¢U +¢(PV) =¢U + nR(T - T )
2
1
-1
3
=-1.78 * 10 J + 2.5 mol * 8.314 J mol K -1
* (268 K - 325 K) =-2.96 kJ

The Reversible Adiabatic Expansion
2.11 and Compression of an Ideal Gas

The adiabatic expansion and compression of gases is an important meteorological
process. For example, the cooling of a cloud as it moves upward in the atmosphere can
be modeled as an adiabatic process because the heat transfer between the cloud and the
rest of the atmosphere is slow on the timescale of its upward motion.
Consider the adiabatic expansion of an ideal gas. Because q = 0 , the first law takes
the form
¢U = w or C dT =-P external dV (2.38)
V
For a reversible adiabatic process, P = P external , and
dV dT dV
C dT =-nRT or, equivalently, C =-nR (2.39)
V
V
V T V
Integrating both sides of this equation between the initial and final states,
T f V f
dT dV
C V =-nR (2.40)
T V
LT i LV i
is constant over the temperature interval T – T , then
If C V f i
T f V f
C ln =-nRln (2.41)
V
T i V i 3
Because C - C = nR for an ideal gas, Equation (2.41) can be written in the form
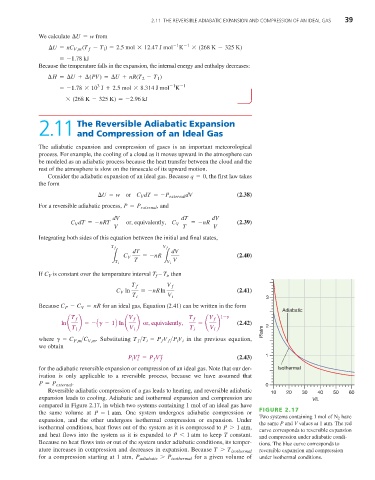
P
V
Adiabatic
T f V f ≤ or, equivalently, T f V f 1-g
ln ¢ ≤ =- Ag - 1B ln ¢ = ¢ ≤ (2.42)
T i V i T i V i P/atm 2
where g = C P,m >C V,m . Substituting T >T = P V >P V in the previous equation,
i i
f
f f
i
we obtain
g
P V = P V g (2.43) 1
f f
i i
for the adiabatic reversible expansion or compression of an ideal gas. Note that our der- Isothermal
ivation is only applicable to a reversible process, because we have assumed that
.
P = P external 0
Reversible adiabatic compression of a gas leads to heating, and reversible adiabatic 10 20 30 40 50 60
expansion leads to cooling. Adiabatic and isothermal expansion and compression are V/L
compared in Figure 2.17, in which two systems containing 1 mol of an ideal gas have
FIGURE 2.17
the same volume at P = 1 atm . One system undergoes adiabatic compression or
expansion, and the other undergoes isothermal compression or expansion. Under Two systems containing 1 mol of N 2 have
the same P and V values at 1 atm. The red
isothermal conditions, heat flows out of the system as it is compressed to P 7 1 atm ,
curve corresponds to reversible expansion
and heat flows into the system as it is expanded to P 6 1 atm to keep T constant.
and compression under adiabatic condi-
Because no heat flows into or out of the system under adiabatic conditions, its temper- tions. The blue curve corresponds to
ature increases in compression and decreases in expansion. Because T 7 T isothermal reversible expansion and compression
for a compression starting at 1 atm, P adiabatic 7 P isothermal for a given volume of under isothermal conditions.