Page 76 - Practical Ship Design

Setting Design Requirements 47

24 1 I I I I I I I
-SUB- HUMP - FORECAST
--*-- CURRENT BEST
Po * POWER REWIRED
TO ATTAIN SPEED

16
014
a
5 12
2
g IO
0
Y
W
p'
26
t-
a
W t-
a SEM1- PLANING
? 4 -
I
9 \

0 I I I I I I 1 I
IO I .5 20 24 30 3.5 4.0 4.5 50 5
Volumetric Froude Number Fu

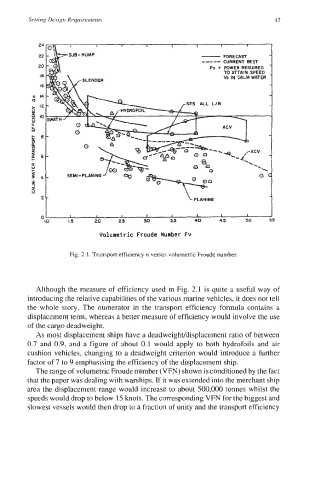
Fig. 2.1. Transport efficiency n versus volumetric Froude number.

Although the measure of efficiency used in Fig. 2.1 is quite a useful way of
introducing the relative capabilities of the various marine vehicles, it does not tell
the whole story. The numerator in the transport efficiency formula contains a
displacement term, whereas a better measure of efficiency would involve the use
of the cargo deadweight.
As most displacement ships have a deadweight/displacement ratio of between
0.7 and 0.9, and a figure of about 0.1 would apply to both hydrofoils and air
cushion vehicles, changing to a deadweight criterion would introduce a further
factor of 7 to 9 emphasising the efficiency of the displacement ship.
The range of volumetric Froude number (VFN) shown is conditioned by the fact
that the paper was dealing with warships. If it was extended into the merchant ship
area the displacement range would increase to about 500,000 tonnes whilst the
speeds would drop to below 15 knots. The corresponding VFN for the biggest and
slowest vessels would then drop to a fraction of unity and the transport efficiency