Page 192 - Pressure Swing Adsorption

' I
166 PRESSURE SWING ADSORPTION

tracking the shock and srmoie waves becomes even more difficult. Further~
more, lhe equilibrium theory approach 1s clearly not applicable to systems in
which seoaratton 1s based on kinetic selectivity.
The alternative route, which 1s discussed in this chapter, 1s to cteveloo a
dynamic simulation model, mciuding the effects of axial m1xmg and mass
transfer resistance. Such dispersive effects are always likely to be oresent in
real systems, even when equilibrium controlled. The dynamic simulatmn
model 1s therefore more realistic and suffic1ently general to be applied for
detailed optmuzation studies of both classes of process. However, unlike the
equilibrium theory approach, dynamic simulation involves tracking the tran•
s1ent by repeated numencal integration of the governmg eauat1ons. This
approach, therefore, provides the advantages of flexibility and greater accu•
racy at the expense of increased comoutation. Both the simpler linear driving I '
~:: E
force (LDF) apprdx1mat1on and more detailed Fickian diffus10n equations I JI·f l
have been used to model the effect of mass transfer resistance. In an I E
eauilibri'Um-controiled process the detailed form of the kinetic model 1s of
only secondary 1moortance, and it 1s found that very little advantage is gamed '
from usmg the more realistic pore diffusion model. Therefore, for equilib·
rium-controlled separatmns the LDF model oroves adequate for all opcrat•
ing conditions, whereas a more detailed mass transfer modei 1s sometimes
necessary for separations based on kinetic select1V1ty. !
I

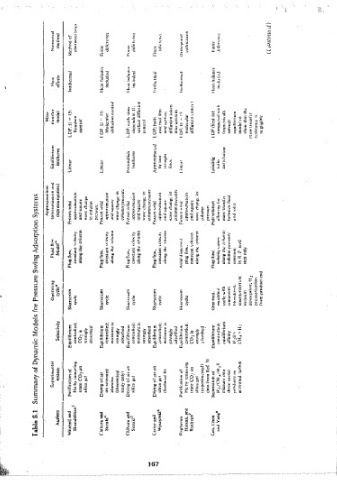
5.1 Summary of the Dynamic Models

The theoretical modeling of a PSA system has been widely studied m order
to gain a clearer understanding of this rather complex process. A summary of
the oublished dynamic models for PSA systems m chronolog1cal order is
compiled in Table 5.1. These models are based on a one• or two-bed process
operated on a Skarstrom cycle or on a modified cycle deoending on the
requirements of the oart1cular system. Because of the transient nature of the
process and the comolexity of the equations describing the system dynamics,
the growth of PSA modeling has followed the route of gradual development
by orogressive elimination of the simolifying restrictions. Starting from very
simple models, which are valid for oniy a few real PSA systems, 1t is now ,,
possible to include an adequate representation of all the more important ~s.r~
factors that may affect performance, and thus to obtam an adequate quanti-
tative model which can be extended to almost any PSA orocess. ti.I!
Detailed numerical simulations have in general been developed only for ,,
single-bed or two-bed systems, but smce the simulation gives the effluent
comoosltion as a function of time, the extension to a multiple-bed process 1s, l
m principle, straightfotward. However, although muitiole-bed systems are l
widely used m mdustry, a detailed reoort of a rnultibed orocess simulation
27
has been published only for hydrogen purification.

!67