Page 107 - Principles and Applications of NanoMEMS Physics

3. NANOMEMS PHYSICS: Quantum Wave Phenomena 95

2
R = π k B 2 χ , (46)
W 2
3 µ γ
B
and captures the degree to which there are electron interaction effects. In
particular, deviations from R signal the presence of interaction. Discussions
W
on the Fermi liquid concept, which embodies phenomena due to electron-
electron interation, usually make use of this index as a characterization
parameter.

3.1.4.2.2 Fermi Liquids

Fermi liquid theory assumes that as the electron-electron interaction is
turned on, from its zero value in the Fermi gas, the states in the now
interacting system evolve directly from those of the noninteracting system,
in such a way that the excited particles may also be labeled by momentum
G G
pairs k, k′ , just as in the noninteracting electron case [134]. This
circumstance is exemplified by the evolution of states in a noninteracting
electron gas situated in an infinite-wall potential well as the interaction
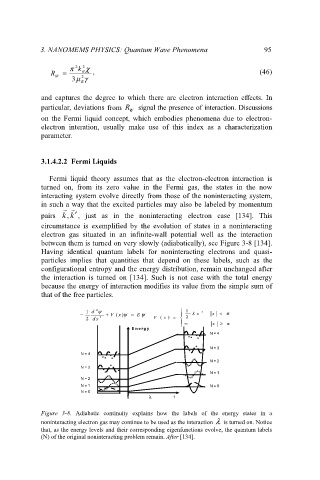
between them is turned on very slowly (adiabatically), see Figure 3-8 [134].
Having identical quantum labels for noninteracting electrons and quasi-
particles implies that quantities that depend on these labels, such as the
configurational entropy and the energy distribution, remain unchanged after
the interaction is turned on [134]. Such is not case with the total energy
because the energy of interaction modifies its value from the simple sum of
that of the free particles.

1 1 d d 2 2 ψ ψ ­ 1 1 2 2
­
<
λ x x
− − + + V x )ψ) ψ = E= E ψ ψ ° ° λ x x < π π
V ( x(
V ( x
2 dx 2 2 V ( x ) ) = = ® 2 2
dx
2
®
≥
° ° ∞ ∞ x x ≥ π π
¯ ¯
En e r g y y
En e r g
N= 4 4
N=
N=
N= 3 3
N=
N= 4 4
N= 2 2
N=
N=
N= 3 3
N=
N= 1 1
N= 2 2
N=
N=
N= 1 1 N=
N= 0 0
N=
N= 0 0
0 0 λ λ 1 1
Figure 3-8. Adiabatic continuity explains how the labels of the energy states in a
noninteracting electron gas may continue to be used as the interaction λ is turned on. Notice
that, as the energy levels and their corresponding eigenfunctions evolve, the quantum labels
(N) of the original noninteracting problem remain. After [134].