Page 252 - Probability and Statistical Inference

4. Functions of Random Variables and Sampling Distribution 229

X ≤ X ≤ ... ≤ X . Define U = Y – Y , V = 1/2(Y + Y ) where recall that
1
n:1
1
n
n:n
n
n:2
U and V are respectively referred to as the range and midrange for the data
X , ..., X . This exercise shows how to derive the pdf of the range, U.
1 n
(i) Show that the joint pdf of Y and Y is given by h(y , y ) = n(n –
1
n
1
n
n–2
1)(y – y ) I(θ < y < y < θ + 1). {Hint: Refer to the equation
n
1
n
1
(4.2.7).};
(ii) Transform (Y , Y ) to (U, V) where U = Y – Y , V = 1/2(Y +
1
n
1
n
n
Y ). Show that the joint pdf of (U, V) is given by g(u, v) = n(n
1
– 1)u when 0 < u < 1, θ + 1/2u < v < θ + 1 – 1/2u, and zero
n–2
otherwise;
(iii) Show that the pdf of U is given by g (u) = n(n – 1)×(1 – u)
1
n–2
u I(0 < u < 1). {Hint:g (u)= ,for 0<u< 1.};
1
(iv) Does the pdf of the range, U, derived in part (iii) correspond to
that of one of the standard random variables from the Section
1.7?

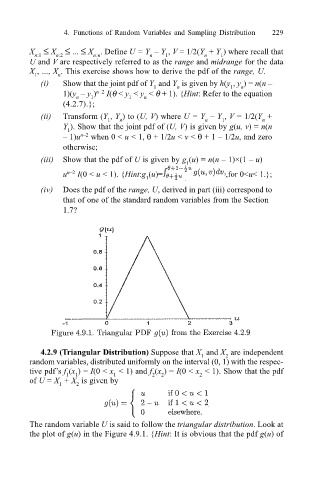
4.2.9 (Triangular Distribution) Suppose that X and X are independent
1
2
random variables, distributed uniformly on the interval (0, 1) with the respec-
tive pdf’s f (x ) = I(0 < x < 1) and f (x ) = I(0 < x < 1). Show that the pdf
1
2
2
1
2
1
of U = X + X is given by
1 2
The random variable U is said to follow the triangular distribution. Look at
the plot of g(u) in the Figure 4.9.1. {Hint: It is obvious that the pdf g(u) of