Page 388 - Probability and Statistical Inference

7. Point Estimation 365

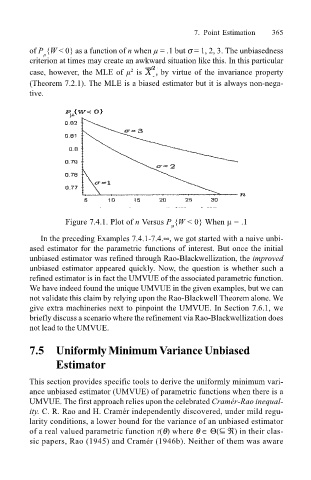
of P {W < 0} as a function of n when µ = .1 but σ = 1, 2, 3. The unbiasedness
µ
criterion at times may create an awkward situation like this. In this particular
2
case, however, the MLE of µ is by virtue of the invariance property
(Theorem 7.2.1). The MLE is a biased estimator but it is always non-nega-
tive.

Figure 7.4.1. Plot of n Versus P {W < 0} When µ = .1
µ
In the preceding Examples 7.4.1-7.4.∞, we got started with a naive unbi-
ased estimator for the parametric functions of interest. But once the initial
unbiased estimator was refined through Rao-Blackwellization, the improved
unbiased estimator appeared quickly. Now, the question is whether such a
refined estimator is in fact the UMVUE of the associated parametric function.
We have indeed found the unique UMVUE in the given examples, but we can
not validate this claim by relying upon the Rao-Blackwell Theorem alone. We
give extra machineries next to pinpoint the UMVUE. In Section 7.6.1, we
briefly discuss a scenario where the refinement via Rao-Blackwellization does
not lead to the UMVUE.

7.5 Uniformly Minimum Variance Unbiased
Estimator

This section provides specific tools to derive the uniformly minimum vari-
ance unbiased estimator (UMVUE) of parametric functions when there is a
UMVUE. The first approach relies upon the celebrated Cramér-Rao inequal-
ity. C. R. Rao and H. Cramér independently discovered, under mild regu-
larity conditions, a lower bound for the variance of an unbiased estimator
⊆
of a real valued parametric function T(θ) where θ ∈ Θ( ℜ) in their clas-
sic papers, Rao (1945) and Cramér (1946b). Neither of them was aware