Page 314 - Schaum's Outline of Differential Equations

CHAP. 30] GAMMA AND BESSEL FUNCTIONS 297

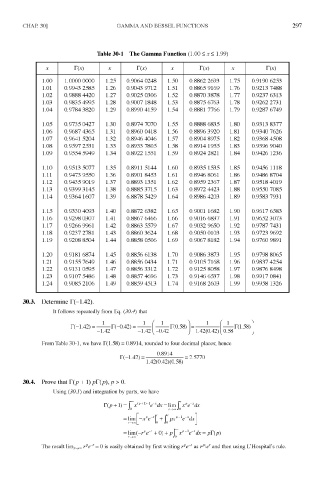
Table 30-1 The Gamma Function (1.00 < x < 1.99)

rc*) r<» rc*) rc*)
X X X X
1.00 1.00000000 1.25 0.9064 0248 1.50 0.8862 2693 1.75 0.9190 6253
1.01 0.9943 2585 1.26 0.9043 9712 1.51 0.8865 9169 1.76 0.9213 7488
1.02 0.98884420 1.27 0.9025 0306 1.52 0.8870 3878 1.77 0.92376313
1.03 0.98354995 1.28 0.9007 1848 1.53 0.8875 6763 1.78 0.92622731
1.04 0.97843820 1.29 0.8990 4159 1.54 0.8881 7766 1.79 0.9287 6749

1.05 0.9735 0427 1.30 0.89747070 1.55 0.8888 6835 1.80 0.9313 8377
1.06 0.96874365 1.31 0.8960 0418 1.56 0.8896 3920 1.81 0.93407626
1.07 0.9641 5204 1.32 0.8946 4046 1.57 0.8904 8975 1.82 0.93684508
1.08 0.95972531 1.33 0.8933 7805 1.58 0.8914 1955 1.83 0.9396 9040
1.09 0.95545949 1.34 0.8922 1551 1.59 0.8924 2821 1.84 0.9426 1236

1.10 0.9513 5077 1.35 0.8911 5144 1.60 0.8935 1535 1.85 0.94561118
1.11 0.9473 9550 1.36 0.8901 8453 1.61 0.8946 8061 1.86 0.9486 8704
1.12 0.9435 9019 1.37 0.8893 1351 1.62 0.8959 2367 1.87 0.95184019
1.13 0.93993145 1.38 0.8885 3715 1.63 0.8972 4423 1.88 0.95507085
1.14 0.9364 1607 1.39 6.8878 5429 1.64 0.8986 4203 1.89 0.95837931

1.15 0.93304093 1.40 0.8872 6382 1.65 0.9001 1682 1.90 0.9617 6583
1.16 0.9298 0307 1.41 0.8867 6466 1.66 0.9016 6837 1.91 0.96523073
1.17 0.9266 9961 1.42 0.8863 5579 1.67 0.9032 9650 1.92 0.97877431
1.18 0.9237 2781 1.43 0.8860 3624 1.68 0.9050 0103 1.93 0.9723 9692
1.19 0.9208 8504 1.44 0.8858 0506 1.69 0.9067 8182 1.94 0.9760 9891

1.20 0.9181 6874 1.45 0.8856 6138 1.70 0.9086 3873 1.95 0.9798 8065
1.21 0.91557649 1.46 0.8856 0434 1.71 0.91057168 1.96 0.98374254
1.22 0.9131 0595 1.47 0.88563312 1.72 0.9125 8058 1.97 0.9876 8498
1.23 0.9107 5486 1.48 0.8857 4696 1.73 0.9146 6537 1.98 0.9917 0841
1.24 0.9085 2106 1.49 0.8859 4513 1.74 0.9168 2603 1.99 0.9958 1326

30.3. Determine r(-1.42).
It follows repeatedly from Eq. (30.4) that

From Table 30-1, we have F(1.58) = 0.8914, rounded to four decimal places; hence

30.4. Prove that T(p + 1) pT(p), p>0.
Using (30.1) and integration by parts, we have

p
p
r
p
r
The result \im r^ co r e = 0 is easily obtained by first writing r e as r le r and then using L'Hospital's rule.