Page 85 - Schaum's Outline of Differential Equations

68 APPLICATIONS OF FIRST-ORDER DIFFERENTIAL EQUATIONS [CHAR 7

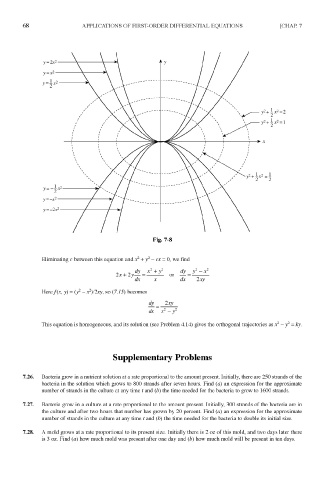
Fig. 7-8

2
1
Eliminating c between this equation and x + y — ex = 0, we find

2
Here/(X y) = (y 2 - x )/2xy, so (7.15) becomes

2
2
This equation is homogeneous, and its solution (see Problem 4.14) gives the orthogonal trajectories as x +y = ky.

Supplementary Problems

7.26. Bacteria grow in a nutrient solution at a rate proportional to the amount present. Initially, there are 250 strands of the
bacteria in the solution which grows to 800 strands after seven hours. Find (a) an expression for the approximate
number of strands in the culture at any time t and (b) the time needed for the bacteria to grow to 1600 strands.

7.27. Bacteria grow in a culture at a rate proportional to the amount present. Initially, 300 strands of the bacteria are in
the culture and after two hours that number has grown by 20 percent. Find (a) an expression for the approximate
number of strands in the culture at any time t and (b) the time needed for the bacteria to double its initial size.

7.28. A mold grows at a rate proportional to its present size. Initially there is 2 oz of this mold, and two days later there
is 3 oz. Find (a) how much mold was present after one day and (b) how much mold will be present in ten days.