Page 111 - Schaum's Outline of Theory and Problems of Applied Physics

96 MOMENTUM [CHAP. 8

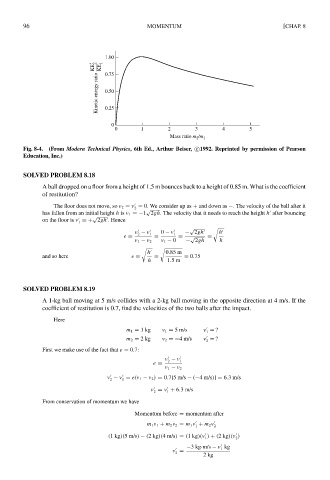
1.00
KE 2 KE 1 0.75
′
Kinetic energy ratio 0.50

0.25

0
0 1 2 3 4 5
/m
Mass ratio m 2 1
Fig. 8-4. (From Modern Technical Physics, 6th Ed., Arthur Beiser, c 1992. Reprinted by permission of Pearson
Education, Inc.)

SOLVED PROBLEM 8.18
A ball dropped on a floor from a height of 1.5 m bounces back to a height of 0.85 m. What is the coefficient
of restitution?

The floor does not move, so v 2 = v = 0. We consider up as + and down as −. The velocity of the ball after it
2 √
has fallen from an initial height h is v 1 =−1 2gh. The velocity that it needs to reach the height h after bouncing

√

on the floor is v =+ 2gh . Hence

1
√

v − v 1 0 − v 1 − 2gh h
2
e = = = √ =
v 1 − v 2 v 1 − 0 − 2gh h

h 0.85 m
and so here e = = = 0.75
h 1.5m
SOLVED PROBLEM 8.19
A 1-kg ball moving at 5 m/s collides with a 2-kg ball moving in the opposite direction at 4 m/s. If the
coefficient of restitution is 0.7, find the velocities of the two balls after the impact.
Here

m 1 = 1kg v 1 = 5 m/s v = ?
1

m 2 = 2kg v 2 =−4 m/s v = ?
2
First we make use of the fact that e = 0.7:

v − v 1
2
e =
v 1 − v 2

v − v = e(v 1 − v 2 ) = 0.7[5 m/s − (−4 m/s)] = 6.3 m/s
2
1

v = v + 6.3 m/s

2
1
From conservation of momentum we have
Momentum before = momentum after
m 1 v 1 + m 2 v 2 = m 1 v + m 2 v

1 2

(1kg)(5 m/s) − (2kg)(4 m/s) = (1kg)(v ) + (2kg)(v )

1 2

−3kg·m/s − v kg
1
v =
2
2kg