Page 152 - Schaum's Outline of Theory and Problems of Applied Physics

CHAP. 11] EQUILIBRIUM 137

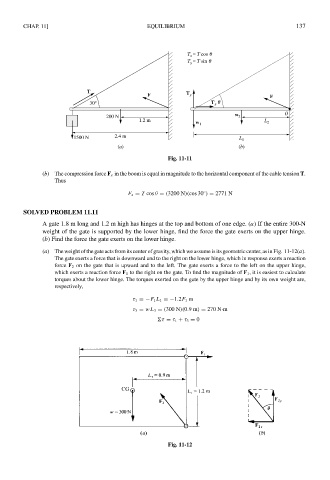
T x = T cos q
= T sin q
T y

T
F T y F
30° T x q
w O
200 N 2
1.2 m L
w 1 2
1500 N 2.4 m L 1
(a) (b)

Fig. 11-11

(b) The compression force F x in the boom is equal in magnitude to the horizontal component of the cable tension T.
Thus
F x = T cos θ = (3200 N)(cos 30 ) = 2771 N
◦

SOLVED PROBLEM 11.11
A gate 1.8 m long and 1.2 m high has hinges at the top and bottom of one edge. (a) If the entire 300-N
weight of the gate is supported by the lower hinge, find the force the gate exerts on the upper hinge.
(b) Find the force the gate exerts on the lower hinge.

(a) The weight of the gate acts from its center of gravity, which we assume is its geometric center, as in Fig. 11-12(a).
The gate exerts a force that is downward and to the right on the lower hinge, which in response exerts a reaction
force F 2 on the gate that is upward and to the left. The gate exerts a force to the left on the upper hinge,
which exerts a reaction force F 1 to the right on the gate. To find the magnitude of F 1 , it is easiest to calculate
torques about the lower hinge. The torques exerted on the gate by the upper hinge and by its own weight are,
respectively,
τ 1 =−F 1 L 1 =−1.2F 1 m
τ 3 = w L 3 = (300 N)(0.9m) = 270 N·m
τ = τ 1 + τ 3 = 0

Fig. 11-12