Page 261 - Schaum's Outline of Theory and Problems of Applied Physics

246 THERMODYNAMICS [CHAP. 21

If the system is a heat engine that operates in a cycle, energy may be stored and released from storage, but
the engine does not undergo a net change in its internal energy during each cycle. In this case

Net heat input = Net work output
The net heat input is the amount of heat Q 1 the engine takes in from the high-temperature reservoir minus the
amount of heat Q 2 the engine gives off to the low-temperature reservoir, as in Fig. 21-1, so that
Q 1 − Q 2 = W

WORK DONE BY AND ON A GAS
The work output of most heat engines is produced by an expanding gas. If the volume of the gas changes from
V 1 to V 2 at the constant pressure p, the work done is
W = p(V 2 − V 1 ) p = constant

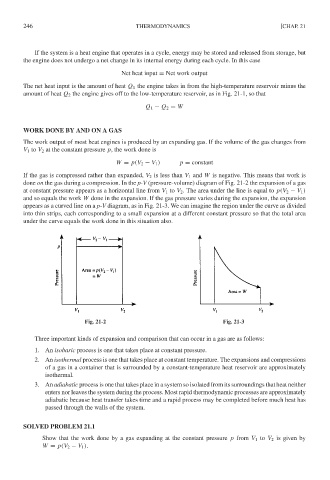
If the gas is compressed rather than expanded, V 2 is less than V 1 and W is negative. This means that work is
done on the gas during a compression. In the p-V (pressure-volume) diagram of Fig. 21-2 the expansion of a gas
at constant pressure appears as a horizontal line from V 1 to V 2 . The area under the line is equal to p(V 2 − V 1 )
and so equals the work W done in the expansion. If the gas pressure varies during the expansion, the expansion
appears as a curved line on a p-V diagram, as in Fig. 21-3. We can imagine the region under the curve as divided
into thin strips, each corresponding to a small expansion at a different constant pressure so that the total area
under the curve equals the work done in this situation also.

Fig. 21-2 Fig. 21-3

Three important kinds of expansion and comparison that can occur in a gas are as follows:
1. An isobaric process is one that takes place at constant pressure.
2. An isothermal process is one that takes place at constant temperature. The expansions and compressions
of a gas in a container that is surrounded by a constant-temperature heat reservoir are approximately
isothermal.
3. An adiabatic process is one that takes place in a system so isolated from its surroundings that heat neither
enters nor leaves the system during the process. Most rapid thermodynamic processes are approximately
adiabatic because heat transfer takes time and a rapid process may be completed before much heat has
passed through the walls of the system.

SOLVED PROBLEM 21.1
Show that the work done by a gas expanding at the constant pressure p from V 1 to V 2 is given by
W = p(V 2 − V 1 ).