Page 358 - Schaum's Outline of Theory and Problems of Applied Physics

CHAP. 28] ELECTROMAGNETIC INDUCTION 343

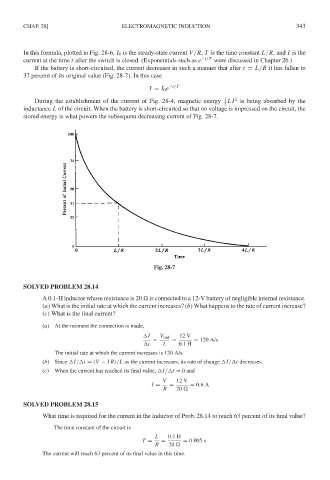
In this formula, plotted in Fig. 28-6, I 0 is the steady-state current V/R, T is the time constant L/R, and I is the
current at the time t after the switch is closed. (Exponentials such as e −t/T were discussed in Chapter 26.)
If the battery is short-circuited, the current decreases in such a manner that after t = L/R it has fallen to
37 percent of its original value (Fig. 28-7). In this case

I = I 0 e −t/T
2
During the establishment of the current of Fig. 28-4, magnetic energy 1 LI is being absorbed by the
2
inductance L of the circuit. When the battery is short-circuited so that no voltage is impressed on the circuit, the
stored energy is what powers the subsequent decreasing current of Fig. 28-7.

Fig. 28-7

SOLVED PROBLEM 28.14
A 0.1-H inductor whose resistance is 20 is connected to a 12-V battery of negligible internal resistance.
(a) What is the initial rate at which the current increases? (b) What happens to the rate of current increase?
(c) What is the final current?
(a) At the moment the connection is made,
I V emf 12 V
= = = 120 A/s
t L 0.1H
The initial rate at which the current increases is 120 A/s.
(b) Since I/ t = (V − IR)/L as the current increases, its rate of change I/ t decreases.
(c) When the current has reached its final value, I/ t = 0 and
V 12 V
I = = = 0.6A
R 20

SOLVED PROBLEM 28.15
What time is required for the current in the inductor of Prob. 28.14 to reach 63 percent of its final value?
The time constant of the circuit is
L 0.1H
T = = = 0.005 s
R 20
The current will reach 63 percent of its final value in this time.