Page 12 - Schaum's Outline of Theory and Problems of Signals and Systems

Chapter 1

Signals and Systems

1.1 INTRODUCTION
The concept and theory of signals and systems are needed in almost all electrical
engineering fields and in many other engineering and scientific disciplines as well. In this
chapter we introduce the mathematical description and representation of signals and
systems and their classifications. We also define several important basic signals essential to
our studies.

1.2 SIGNALS AND CLASSIFICATION OF SIGNALS

A signal is a function representing a physical quantity or variable, and typically it
contains information about the behavior or nature of the phenomenon. For instance, in a
RC circuit the signal may represent the voltage across the capacitor or the current flowing
in the resistor. Mathematically, a signal is represented as a function of an independent
variable t. Usually t represents time. Thus, a signal is denoted by x(t).

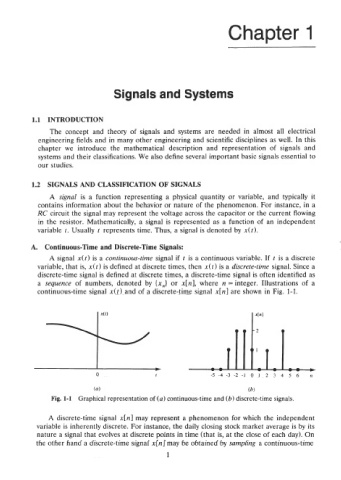
A. Continuous-Time and Discrete-Time Signals:
A signal x(t) is a continuous-time signal if t is a continuous variable. If t is a discrete
variable, that is, x(t) is defined at discrete times, then x(t) is a discrete-time signal. Since a
discrete-time signal is defined at discrete times, a discrete-time signal is often identified as
a sequence of numbers, denoted by {x,) or x[n], where n = integer. Illustrations of a
continuous-time signal x(t) and of a discrete-time signal x[n] are shown in Fig. 1-1.

(4 (b)
Fig. 1-1 Graphical representation of (a) continuous-time and (6) discrete-time signals.

A discrete-time signal x[n] may represent a phenomenon for which the independent
variable is inherently discrete. For instance, the daily closing stock market average is by its
nature a signal that evolves at discrete points in time (that is, at the close of each day). On
the other hand a discrete-time signal x[n] may be obtained by sampling a continuous-time

1