Page 289 - Schaum's Outline of Theory and Problems of Signals and Systems

FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS [CHAP. 5

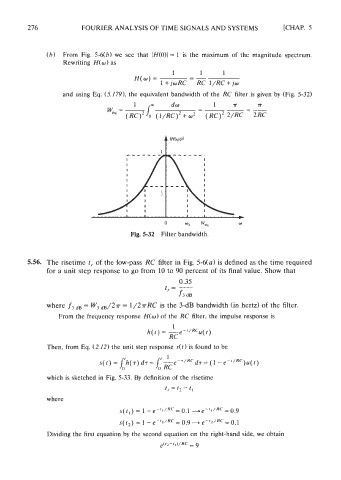
(6) From Fig. 5-6(b) we see that IH(O)I = 1 is the maximum of the magnitude spectrum.
Rewriting H(w) as

and using Eq. (5.179), the equivalent bandwidth of the RC filter is given by (Fig. 5-32)

0 Wa Weq w
Fig. 5-32 Filter bandwidth.

5.56. The risetime t, of the low-pass RC filter in Fig. 5-6(a) is defined as the time required
for a unit step response to go from 10 to 90 percent of its final value. Show that

where f, ,, = W, ,,/2.rr = 1/2.rrRC is the 3-dB bandwidth (in hertz) of the filter.
From the frequency response H(w) of the RC filter, the impulse response is

Then, from Eq. (2.12) the unit step response dt) is found to be

Dividing the first equation by the second equation on the right-hand side, we obtain
e(r~-rd/RC = 9