Page 145 - Probability, Random Variables and Random Processes

CHAP. 41 FUNCTIONS OF RANDOM VARIABLES, EXPECTATION, LIMIT THEOREMS 137

Fig. 4-6

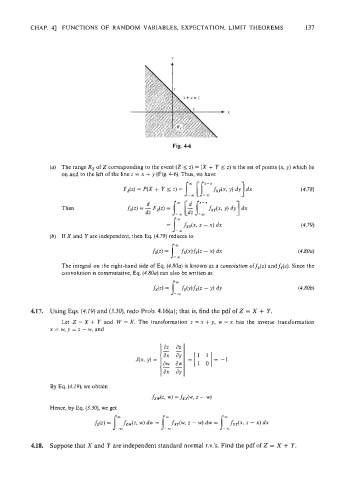
(a) The range Rz of Z corresponding to the event (Z I z) = (X + Y I z) is the set of points (x, y) which lie
on and to the left of the line z = x + y (Fig. 4-6). Thus, we have

Then
= J=Im
fx.,,
dx
x)
-
2
(b) If X and Y are independent, then Eq. (4.79) reduces to
The integral on the right-hand side of Eq. (4.80~) is known as a convolution of f,(z) and fdz). Since the
convolution is commutative, Eq. (4.80~) can also be written as

4.17. Using Eqs. (4.1 9) and (3.30), redo Prob. 4.16(a); that is, find the pdf of Z = X + Y.
Let Z = X + Y and W = X. The transformation z = x + y, w = x has the inverse transformation
x=w,y=z-w,and

By Eq. (4.19), we obtain

Hence, by Eq. (3.30), we get

4.18. Suppose that X and Y are independent standard normal r.v.'s. Find the pdf of Z = X + Y.