Page 299 - Theory and Problems of BEGINNING CHEMISTRY

288 NUCLEAR REACTIONS [CHAP. 19

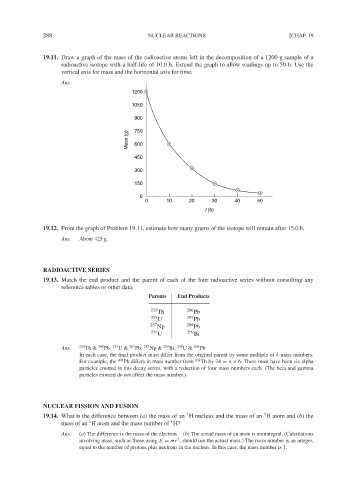
19.11. Draw a graph of the mass of the radioactive atoms left in the decomposition of a 1200-g sample of a
radioactive isotope with a half-life of 10.0 h. Extend the graph to allow readings up to 50 h. Use the
vertical axis for mass and the horizontal axis for time.
Ans.
1200

1050

900

Mass (g) 750
600

450
300

150

0
0 10 20 30 40 50
t (h)

19.12. From the graph of Problem 19.11, estimate how many grams of the isotope will remain after 15.0 h.
Ans. About 425 g.

RADIOACTIVE SERIES
19.13. Match the end product and the parent of each of the four radioactive series without consulting any
reference tables or other data.
Parents End Products

232 206
Th Pb
235 207
U Pb
237 208
Np Pb
238 209
U Bi
Ans. 232 Th & 208 Pb; 235 U& 207 Pb; 237 Np & 209 Bi; 238 U& 206 Pb
In each case, the final product must differ from the original parent by some multiple of 4 mass numbers.
For example, the 208 Pb differs in mass number from 232 Th by 24 = 4 × 6. There must have been six alpha
particles emitted in this decay series, with a reduction of four mass numbers each. (The beta and gamma
particles emitted do not affect the mass number.)

NUCLEAR FISSION AND FUSION
1
1
19.14. What is the difference between (a) the mass of an H nucleus and the mass of an H atom and (b) the
1
1
mass of an H atom and the mass number of H?
Ans. (a) The difference is the mass of the electron. (b) The actual mass of an atom is nonintegral. (Calculations
2
involving mass, such as those using E = mc , should use the actual mass.) The mass number is an integer,
equal to the number of protons plus neutrons in the nucleus. In this case, the mass number is 1.