Page 102 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

Quantum Mechanics of Single Electrons
vector x is the center of mass. For the electron described in terms of a
wavefunction it is the average value of its position
∫
(
,
Ψ x ˆ Ψ〉
(
,
x ˆ 〈〉 = Ψ∗ x t)x ˆ Ψ x t) = 〈| (3.3)
Ω
ˆ
x ˆ
In this case is called the position operator. We shall use to identify
operators whenever we are not dealing with a special representation. In
x ˆ
the position representation is a vector with cartesian components x, y
and z.
Expectation The result of (3.3) gives the most probable position where to find a parti-
Values cle. It is called the expectation value of the position operator. It is possi-
ble to calculate the expectation values of arbitrary functions of , such
x ˆ
as the variance of the position, which gives us important information
about the spreading of the wavefunction

2
2
Ψ x ˆ 〈〉) Ψ〉 =
Var x() = ( 〈 ∆x ˆ ) 〉 = 〈| ( – x ˆ 2 〈| ( 2 x ˆ 〈〉 )Ψ〉 (3.4)
Ψ x ˆ –
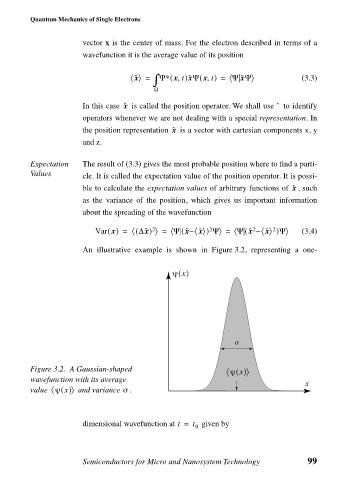
An illustrative example is shown in Figure 3.2, representing a one-
ψ x ()

σ

Figure 3.2. A Gaussian-shaped 〈 ψ x()〉
wavefunction with its average
x
value ψ x()〉 and variance .
〈
σ

dimensional wavefunction at t = t given by
0

Semiconductors for Micro and Nanosystem Technology 99