Page 189 - Sensing, Intelligence, Motion : How Robots and Humans Move in an Unstructured World

164 ACCOUNTING FOR BODY DYNAMICS: THE JOGGER’S PROBLEM

4.3.3 Dynamics and Collision Avoidance
Consider a time sequence σ t ={t 0 ,t 1 ,t 2 ,... , } of the starting moments of steps.
Step i takes place within the interval [t i ,t i+1 ), (t i+1 − t i ) = δt.Atmoment t i the
robot is at the position C i , with the velocity vector V i . Within this interval, based
on the sensing data, intermediate target T i (supplied by the kinematic planning
algorithm), and vector V i , the control system will calculate the values of control
forces p and q. The forces are then applied to the robot, and the robot executes
step i, finishing it at point C i+1 at moment t i+1 , with the velocity vector V i+1 .
Then the process repeats.
Analysis that leads to the procedure for handling dynamics consists of three
parts. First, in the remainder of this section we incorporate the control constraints
into the robot’s model and develop transformations between the primary path
frame and world frame and between the secondary path frame and world frame.
Then in Section 4.3.4 we develop the canonical solution. Finally, in Section 4.3.5
we develop the near-canonical solution, for the case when the canonical solution
would result in a collision. The resulting algorithm operates incrementally; forces
p and q are computed at each step. The remainder of this section refers to the
time interval [t i ,t i+1 ) and its intermediate target T i , and so index i is often
dropped.
2
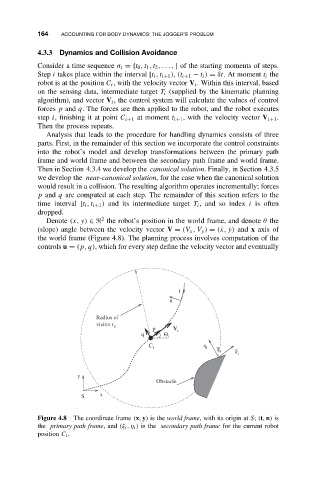
Denote (x, y) ∈ the robot’s position in the world frame, and denote θ the
(slope) angle between the velocity vector V = (V x ,V y ) = (˙x, ˙y) and x axis of
the world frame (Figure 4.8). The planning process involves computation of the
controls u = (p, q), which for every step define the velocity vector and eventually

t
n

Radius of
vision r u
p V i
q Θ i
C h
i
i
T i x i
y
Obstacle
S x

Figure 4.8 The coordinate frame (x, y) is the world frame, with its origin at S; (t, n) is
the primary path frame,and (ξ i ,η i ) is the secondary path frame for the current robot
position C i .