Page 122 -

CHAPTER 4 SOFTWARE PROCESS AND PROJECT METRICS 93

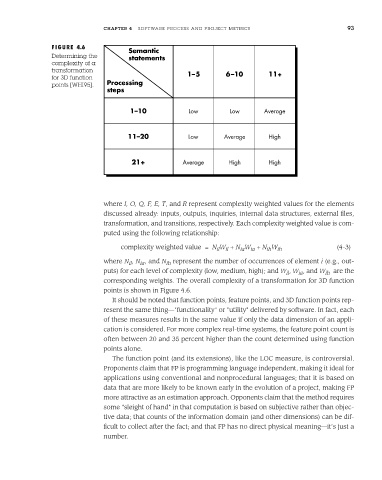
FIGURE 4.6
Semantic
Determining the statements
complexity of a
transformation
1–5 6–10 11+
for 3D function
Processing
points [WHI95].
steps
1–10 Low Low Average

11–20 Low Average High

21+ Average High High

where I, O, Q, F, E, T, and R represent complexity weighted values for the elements
discussed already: inputs, outputs, inquiries, internal data structures, external files,
transformation, and transitions, respectively. Each complexity weighted value is com-
puted using the following relationship:
complexity weighted value = N W + N W + N W ih (4-3)
ia
ih
il
ia
il
where N , N , and N ih represent the number of occurrences of element i (e.g., out-
ia
il
puts) for each level of complexity (low, medium, high); and W , W , and W ih are the
il
ia
corresponding weights. The overall complexity of a transformation for 3D function
points is shown in Figure 4.6.
It should be noted that function points, feature points, and 3D function points rep-
resent the same thing—"functionality" or "utility" delivered by software. In fact, each
of these measures results in the same value if only the data dimension of an appli-
cation is considered. For more complex real-time systems, the feature point count is
often between 20 and 35 percent higher than the count determined using function
points alone.
The function point (and its extensions), like the LOC measure, is controversial.
Proponents claim that FP is programming language independent, making it ideal for
applications using conventional and nonprocedural languages; that it is based on
data that are more likely to be known early in the evolution of a project, making FP
more attractive as an estimation approach. Opponents claim that the method requires
some "sleight of hand" in that computation is based on subjective rather than objec-
tive data; that counts of the information domain (and other dimensions) can be dif-
ficult to collect after the fact; and that FP has no direct physical meaning—it's just a
number.