Page 16 - STATISTICAL MECHANICS: From First Principles to Macroscopic Phenomena

2 Introduction

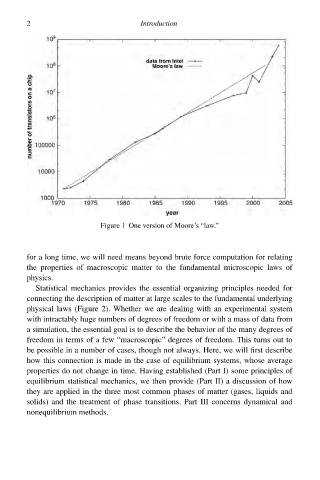
Figure 1 One version of Moore’s “law.”

for a long time, we will need means beyond brute force computation for relating
the properties of macroscopic matter to the fundamental microscopic laws of
physics.
Statistical mechanics provides the essential organizing principles needed for
connecting the description of matter at large scales to the fundamental underlying
physical laws (Figure 2). Whether we are dealing with an experimental system
with intractably huge numbers of degrees of freedom or with a mass of data from
a simulation, the essential goal is to describe the behavior of the many degrees of
freedom in terms of a few “macroscopic” degrees of freedom. This turns out to
be possible in a number of cases, though not always. Here, we will first describe
how this connection is made in the case of equilibrium systems, whose average
properties do not change in time. Having established (Part I) some principles of
equilibrium statistical mechanics, we then provide (Part II) a discussion of how
they are applied in the three most common phases of matter (gases, liquids and
solids) and the treatment of phase transitions. Part III concerns dynamical and
nonequilibrium methods.