Page 176 - Understanding Flight

CH06_Anderson 7/25/01 8:59 AM Page 163

High-Speed Flight 163

70
60

50
Sweep angle 40

30

20

10
1.07 2 3
0
0.5 1.0 1.5 2.0 2.5 3.0 3.5
Mach no.
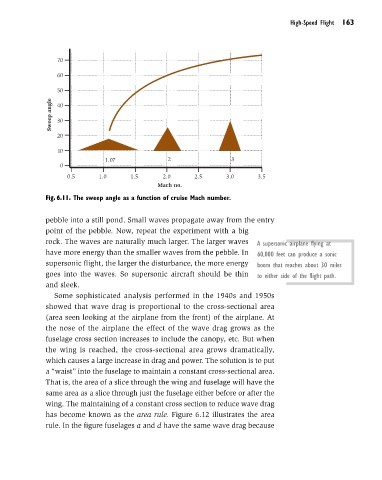
Fig. 6.11. The sweep angle as a function of cruise Mach number.

pebble into a still pond. Small waves propagate away from the entry
point of the pebble. Now, repeat the experiment with a big
rock. The waves are naturally much larger. The larger waves A supersonic airplane flying at
have more energy than the smaller waves from the pebble. In 60,000 feet can produce a sonic
supersonic flight, the larger the disturbance, the more energy boom that reaches about 30 miles
goes into the waves. So supersonic aircraft should be thin to either side of the flight path.
and sleek.
Some sophisticated analysis performed in the 1940s and 1950s
showed that wave drag is proportional to the cross-sectional area
(area seen looking at the airplane from the front) of the airplane. At
the nose of the airplane the effect of the wave drag grows as the
fuselage cross section increases to include the canopy, etc. But when
the wing is reached, the cross-sectional area grows dramatically,
which causes a large increase in drag and power. The solution is to put
a “waist” into the fuselage to maintain a constant cross-sectional area.
That is, the area of a slice through the wing and fuselage will have the
same area as a slice through just the fuselage either before or after the
wing. The maintaining of a constant cross section to reduce wave drag
has become known as the area rule. Figure 6.12 illustrates the area
rule. In the figure fuselages a and d have the same wave drag because