Page 105 - Mechanical Behavior of Materials

106 Chapter 3 A Survey of Engineering Materials

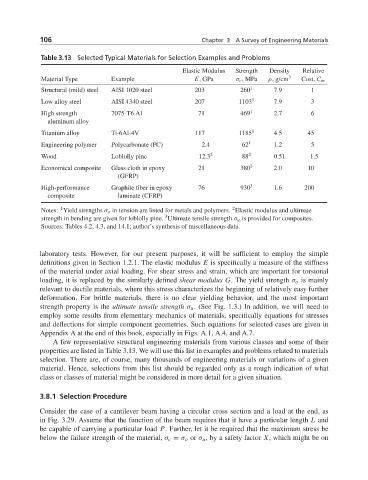
Table 3.13 Selected Typical Materials for Selection Examples and Problems

Elastic Modulus Strength Density Relative
Material Type Example E, GPa σ c , MPa ρ, g/cm 3 Cost, C m
Structural (mild) steel AISI 1020 steel 203 260 1 7.9 1
Low alloy steel AISI 4340 steel 207 1103 1 7.9 3
High strength 7075-T6 Al 71 469 1 2.7 6
aluminum alloy
Titanium alloy Ti-6Al-4V 117 1185 1 4.5 45
Engineering polymer Polycarbonate (PC) 2.4 62 1 1.2 5
Wood Loblolly pine 12.3 2 88 2 0.51 1.5
Economical composite Glass cloth in epoxy 21 380 3 2.0 10
(GFRP)
High-performance Graphite fiber in epoxy 76 930 3 1.6 200
composite laminate (CFRP)
2
1
Notes: Yield strengths σ o in tension are listed for metals and polymers. Elastic modulus and ultimate
3
strength in bending are given for loblolly pine. Ultimate tensile strength σ u is provided for composites.
Sources: Tables 4.2, 4.3, and 14.1; author’s synthesis of miscellaneous data.

laboratory tests. However, for our present purposes, it will be sufficient to employ the simple
definitions given in Section 1.2.1. The elastic modulus E is specifically a measure of the stiffness
of the material under axial loading. For shear stress and strain, which are important for torsional
loading, it is replaced by the similarly defined shear modulus G. The yield strength σ o is mainly
relevant to ductile materials, where this stress characterizes the beginning of relatively easy further
deformation. For brittle materials, there is no clear yielding behavior, and the most important
strength property is the ultimate tensile strength σ u . (See Fig. 1.3.) In addition, we will need to
employ some results from elementary mechanics of materials, specifically equations for stresses
and deflections for simple component geometries. Such equations for selected cases are given in
Appendix A at the end of this book, especially in Figs. A.1, A.4, and A.7.
A few representative structural engineering materials from various classes and some of their
properties are listed in Table 3.13. We will use this list in examples and problems related to materials
selection. There are, of course, many thousands of engineering materials or variations of a given
material. Hence, selections from this list should be regarded only as a rough indication of what
class or classes of material might be considered in more detail for a given situation.

3.8.1 Selection Procedure

Consider the case of a cantilever beam having a circular cross section and a load at the end, as
in Fig. 3.29. Assume that the function of the beam requires that it have a particular length L and
be capable of carrying a particular load P. Further, let it be required that the maximum stress be
below the failure strength of the material, σ c = σ o or σ u , by a safety factor X, which might be on