Page 344 - Mechanical Behavior of Materials

Section 8.3 Mathematical Concepts 345

8.3.1 Strain Energy Release Rate, G

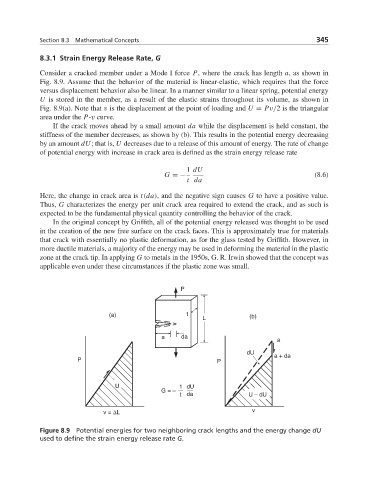
Consider a cracked member under a Mode I force P, where the crack has length a,asshown in
Fig. 8.9. Assume that the behavior of the material is linear-elastic, which requires that the force
versus displacement behavior also be linear. In a manner similar to a linear spring, potential energy
U is stored in the member, as a result of the elastic strains throughout its volume, as shown in
Fig. 8.9(a). Note that v is the displacement at the point of loading and U = Pv/2 is the triangular
area under the P-v curve.
If the crack moves ahead by a small amount da while the displacement is held constant, the
stiffness of the member decreases, as shown by (b). This results in the potential energy decreasing
by an amount dU; that is, U decreases due to a release of this amount of energy. The rate of change
of potential energy with increase in crack area is defined as the strain energy release rate
1 dU
G =− (8.6)
t da
Here, the change in crack area is t(da), and the negative sign causes G to have a positive value.
Thus, G characterizes the energy per unit crack area required to extend the crack, and as such is
expected to be the fundamental physical quantity controlling the behavior of the crack.
In the original concept by Griffith, all of the potential energy released was thought to be used
in the creation of the new free surface on the crack faces. This is approximately true for materials
that crack with essentially no plastic deformation, as for the glass tested by Griffith. However, in
more ductile materials, a majority of the energy may be used in deforming the material in the plastic
zone at the crack tip. In applying G to metals in the 1950s, G. R. Irwin showed that the concept was
applicable even under these circumstances if the plastic zone was small.

P

(a) t (b)
L

a da
a
dU
P P a + da

U 1 dU
G = –
t da U – dU
v = ΔL v

Figure 8.9 Potential energies for two neighboring crack lengths and the energy change dU
used to define the strain energy release rate G.