Page 257 - Introduction to Statistical Pattern Recognition

5 Parameter Estimation 239

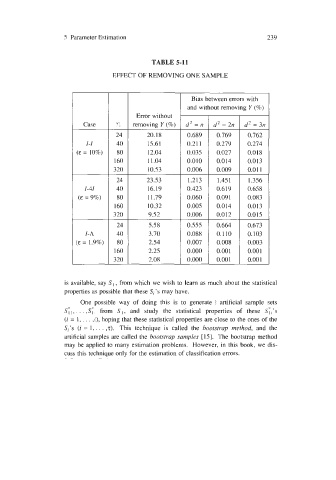
TABLE 5-11

EFFECT OF REMOVING ONE SAMPLE

Bias between errors with
and without removing Y (%)
Error without
Case removing Y (%) d2 =n d2 =2n I d2 =3n
24 20.18 0.689 0.769 0.762
1-1 40 15.61 0.21 1 0.279 0.274
(E = 10%) 80 12.04 0.035 0.027 0.018
160 11.04 0.010 0.014 0.013
320 10.53 0.006 0.009 0.01 1
23.53 1.213 1.45 1 1.356
1-41 16.19 0.423 0.619 0.658
(E = 9%) 11.79 0.060 0.001 t 0.09 1 0.083
10.32 0.005 0.014 0.013
9.52 0.006 0.012 0.015
5.58 0.555 0.664 0.673
I-A 3.70 0.088 0.110 0.103
(E = 1.9%) 2.54 0.007 0.008 0.003
2.25 0.000 0.001 0.00 1
2.08 0.000 0.00 1

is available, say SI, from which we wish to learn as much about the statistical
properties as possible that these S, ’s may have.
One possible way of doing this is to generate t artificial sample sets
S;, , . . . ,S; from S1, and study the statistical properties of these S;,’s
(i = 1, . . . ,t), hoping that these statistical properties are close to the ones of the
S,’s (i = 1, . . . ,T). This technique is called the bootstrap method, and the
artificial samples are called the bootstrap samples [ 151. The bootstrap method
may be applied to many estimation problems. However, in this book, we dis-
cuss this technique only for the estimation of classification errors.