Page 205 - 3D Fibre Reinforced Polymer Composites

194 30 Fibre Reinforced Polymer Composites

considered in the models, leading to predictions of the ultimate strength of the bridging
ligaments in mixed mode conditions.

-

0
7 8
Measured GI,, (kJ/m2)
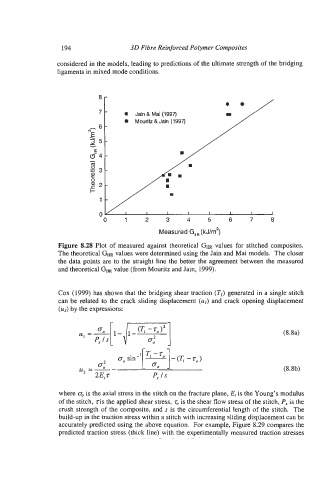
Figure 8.28 Plot of measured against theoretical GIIR values for stitched composites.
The theoretical GIIR values were determined using the Jain and Mai models. The closer
the data points are to the straight line the better the agreement between the measured
and theoretical GllR value (from Mouritz and Jain, 1999).

Cox (1999) has shown that the bridging shear traction (TI) generated in a single stitch
can be related to the crack sliding displacement (u,) and crack opening displacement
(uj) by the expressions:

(8.8a)

(8.8b)

where a, is the axial stress in the stitch on the fracture plane, E, is the Young’s modulus
of the stitch, Tis the applied shear stress, z, is the shear flow stress of the stitch, P, is the
crush strength of the composite, and s is the circumferential length of the stitch. The
build-up in the traction stress within a stitch with increasing sliding displacement can be
accurately predicted using the above equation. For example, Figure 8.29 compares the
predicted traction stress (thick line) with the experimentally measured traction stresses