Page 283 - ARM 64 Bit Assembly Language

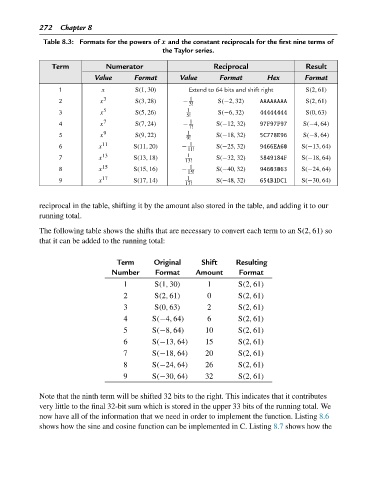
272 Chapter 8

Table 8.3: Formats for the powers of x and the constant reciprocals for the first nine terms of
the Taylor series.

Term Numerator Reciprocal Result
Value Format Value Format Hex Format
1 x S(1,30) Extend to 64 bits and shift right S(2,61)
2 x 3 S(3,28) − 1 S(−2,32) AAAAAAAA S(2,61)
3!
3 x 5 S(5,26) 1 S(−6,32) 44444444 S(0,63)
5!
4 x 7 S(7,24) − 1 S(−12,32) 97F97F97 S(−4,64)
7!
5 x 9 S(9,22) 1 S(−18,32) 5C778E96 S(−8,64)
9!
6 x 11 S(11,20) − 1 S(−25,32) 9466EA60 S(−13,64)
11!
7 x 13 S(13,18) 1 S(−32,32) 5849184F S(−18,64)
13!
8 x 15 S(15,16) − 1 S(−40,32) 94603063 S(−24,64)
15!
9 x 17 S(17,14) 1 S(−48,32) 654B1DC1 S(−30,64)
17!

reciprocal in the table, shifting it by the amount also stored in the table, and adding it to our
running total.
The following table shows the shifts that are necessary to convert each term to an S(2,61) so
that it can be added to the running total:

Term Original Shift Resulting
Number Format Amount Format
1 S(1,30) 1 S(2,61)
2 S(2,61) 0 S(2,61)
3 S(0,63) 2 S(2,61)
4 S(−4,64) 6 S(2,61)
5 S(−8,64) 10 S(2,61)
6 S(−13,64) 15 S(2,61)
7 S(−18,64) 20 S(2,61)
8 S(−24,64) 26 S(2,61)
9 S(−30,64) 32 S(2,61)

Note that the ninth term will be shifted 32 bits to the right. This indicates that it contributes
very little to the final 32-bit sum which is stored in the upper 33 bits of the running total. We
now have all of the information that we need in order to implement the function. Listing 8.6
shows how the sine and cosine function can be implemented in C. Listing 8.7 shows how the