Page 252 - Adaptive Identification and Control of Uncertain Systems with Nonsmooth Dynamics

Hysteresis Dynamics and Modeling 253

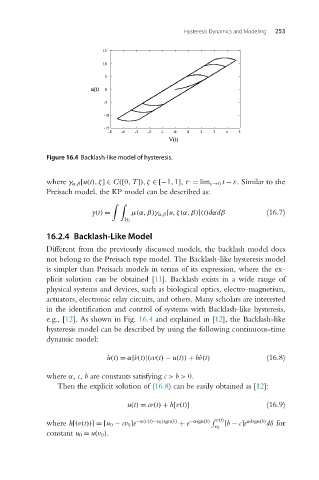
Figure 16.4 Backlash-like model of hysteresis.

_
where γ α,β [u(t),ζ]∈ C([0,T]),ζ ∈[−1,1], t = lim ε→0 t − ε. Similar to the
Preisach model, the KP model can be described as:

y(t) = μ(α,β)γ α,β [u,ζ(α,β)](t)dαdβ (16.7)
P 0
16.2.4 Backlash-Like Model

Different from the previously discussed models, the backlash model does
not belong to the Preisach type model. The Backlash-like hysteresis model
is simpler than Preisach models in terms of its expression, where the ex-
plicit solution can be obtained [11]. Backlash exists in a wide range of
physical systems and devices, such as biological optics, electro-magnetism,
actuators, electronic relay circuits, and others. Many scholars are interested
in the identification and control of systems with Backlash-like hysteresis,
e.g., [12]. As shown in Fig. 16.4 and explained in [12], the Backlash-like
hysteresis model can be described by using the following continuous-time
dynamic model:

˙ u(t) = α|˙v(t)|(cv(t) − u(t)) + b˙v(t) (16.8)

where α, c, b are constants satisfying c > b > 0.
Then the explicit solution of (16.8) can be easily obtained as [12]:

u(t) = cv(t) + h[v(t)] (16.9)

where h[(v(t))]=[u 0 − cv 0 ]e −α(v(t)−v 0 )sgn(˙v) + e −αsgn(˙v) v(t) [b − c]e αδsgn(˙v) dδ for
v 0
constant u 0 = u(v 0 ).