Page 217 - Adsorbents fundamentals and applications

202 π-COMPLEXATION SORBENTS AND APPLICATIONS

1.2

1.0
Amount adsorbed (mmol/g) 0.8 C H on Ag resin

0.6
+
2
4
0.4
4
C 2
H on resin (Amberlyst 15)
C 2
6
+
H on Ag resin
6
C 2 H on resin (Amberlyst 15)
0.2
0.0
0.0 0.2 0.4 0.6 0.8 1.0
Pressure (atm)
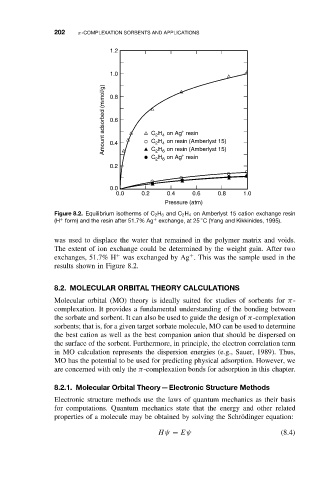
Figure 8.2. Equilibrium isotherms of C 2 H 6 and C 2 H 4 on Amberlyst 15 cation exchange resin
◦
+
+
(H form) and the resin after 51.7% Ag exchange, at 25 C (Yang and Kikkinides, 1995).
was used to displace the water that remained in the polymer matrix and voids.
The extent of ion exchange could be determined by the weight gain. After two
exchanges, 51.7% H was exchanged by Ag . This was the sample used in the
+
+
results shown in Figure 8.2.
8.2. MOLECULAR ORBITAL THEORY CALCULATIONS
Molecular orbital (MO) theory is ideally suited for studies of sorbents for π-
complexation. It provides a fundamental understanding of the bonding between
the sorbate and sorbent. It can also be used to guide the design of π-complexation
sorbents; that is, for a given target sorbate molecule, MO can be used to determine
the best cation as well as the best companion anion that should be dispersed on
the surface of the sorbent. Furthermore, in principle, the electron correlation term
in MO calculation represents the dispersion energies (e.g., Sauer, 1989). Thus,
MO has the potential to be used for predicting physical adsorption. However, we
are concerned with only the π-complexation bonds for adsorption in this chapter.

8.2.1. Molecular Orbital Theory—Electronic Structure Methods
Electronic structure methods use the laws of quantum mechanics as their basis
for computations. Quantum mechanics state that the energy and other related
properties of a molecule may be obtained by solving the Schr¨ odinger equation:

Hψ = Eψ (8.4)