Page 166 - Adsorption Technology & Design, Elsevier (1998)

154 Design procedures

Equations (6.19) and (6.34)-(6.36) must be solved simultaneously with an
appropriate rate expression which must be consistent with the equilibrium
isotherm which describes the adsorption. Table 6.1 summarizes the sources

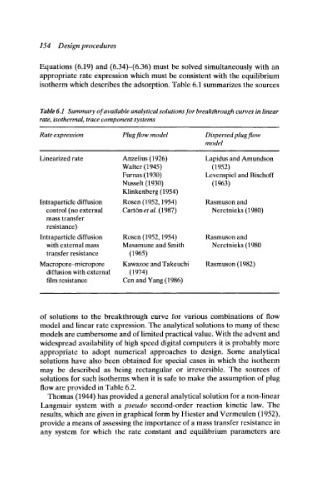
Table 6.1 Summary of available analytical solutions for breakthrough curves in linear
rate, isothermal, trace component systems
Rate expression Plug flow model Dispersed plug flow
model
Linearized rate Anzelius (1926) Lapidus and Amundson
Walter (1945) (1952)
Furnas (1930) Levenspiel and Bischoff
Nusselt (1930) (1963)
Klinkenberg (1954)
Intraparticle diffusion Rosen (1952,1954) Rasmuson and
control (no external Cart6n et al. (1987) Neretnieks (1980)
mass transfer
resistance)
Intraparticle diffusion Rosen (1952, 1954) Rasmuson and
with external mass Masamune and Smith Neretnieks (| 980
transfer resistance (1965)
Macropore-micropore Kawazoe and Takeuchi Rasmuson (1982)
diffusion with external (1974)
film resistance Cen and Yang (1986)

of solutions to the breakthrough curve for various combinations of flow
model and linear rate expression. The analytical solutions to many of these
models are cumbersome and of limited practical value. With the advent and
widespread availability of high speed digital computers it is probably more
appropriate to adopt numerical approaches to design. Some analytical
solutions have also been obtained for special cases in which the isotherm
may be described as being rectangular or irreversible. The sources of
solutions for such isotherms when it is safe to make the assumption of plug
flow are provided in Table 6.2.
Thomas (1944) has provided a general analytical solution for a non-linear
Langmuir system with a pseudo second-order reaction kinetic law. The
results, which are given in graphical form by Hiester and Vermeulen (1952),
provide a means of assessing the importance of a mass transfer resistance in
any system for which the rate constant and equilibrium parameters are