Page 37 - Adsorption Technology & Design, Elsevier (1998)

34 Fundamentals of adsorption equilibria

IV

"0
(1)
-E
o
r
"1o
r
:3
0
E
<
i
Ps Ps Ps
Pressure,,,

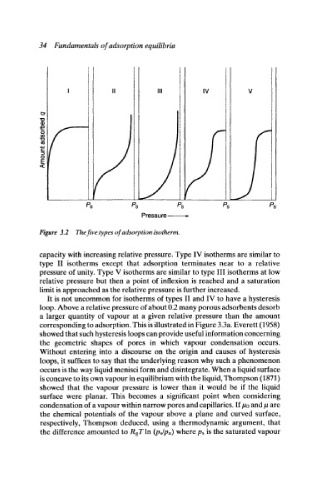
Figure 3.2 The five types of adsorption isotherm.

capacity with increasing relative pressure. Type IV isotherms are similar to
type II isotherms except that adsorption terminates near to a relative
pressure of unity. Type V isotherms are similar to type III isotherms at low
relative pressure but then a point of inflexion is reached and a saturation
limit is approached as the relative pressure is further increased.
It is not uncommon for isotherms of types II and IV to have a hysteresis
loop. Above a relative pressure of about 0.2 many porous adsorbents desorb
a larger quantity of vapour at a given relative pressure than the amount
corresponding to adsorption. This is illustrated in Figure 3.3a. Everett (1958)
showed that such hysteresis loops can provide useful information concerning
the geometric shapes of pores in which vapour condensation occurs.
Without entering into a discourse on the origin and causes of hysteresis
loops, it suffices to say that the underlying reason why such a phenomenon
occurs is the way liquid menisci form and disintegrate. When a liquid surface
is concave to its own vapour in equilibrium with the liquid, Thompson (1871)
showed that the vapour pressure is lower than it would be if the liquid
surface were planar. This becomes a significant point when considering
condensation of a vapour within narrow pores and capillaries. If/z0 and/z are
the chemical potentials of the vapour above a plane and curved surface,
respectively, Thompson deduced, using a thermodynamic argument, that
the difference amounted to RgT In (ps/pa) where ps is the saturated vapour