Page 548 - Advanced_Engineering_Mathematics o'neil

528 CHAPTER 15 Special Functions and Eigenfunction Expansions

1

0.5

x
0
–2 –1 0 1 2

–0.5

–1

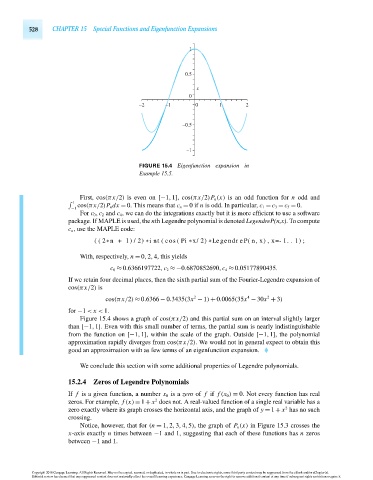
FIGURE 15.4 Eigenfunction expansion in
Example 15.5.

First, cos(πx/2) is even on [−1,1], cos(πx/2)P n (x) is an odd function for n odd and
1
cos(πx/2)P n dx = 0. This means that c n = 0if n is odd. In particular, c 1 = c 3 = c 5 = 0.
−1
For c 0 ,c 2 and c 4 , we can do the integrations exactly but it is more efficient to use a software
package. If MAPLE is used, the nth Legendre polynomial is denoted LegendreP(n,x). To compute
c n , use the MAPLE code:
((2 * n + 1)/2) * int(cos(Pi * x/2) * LegendreP(n,x),x=-1..1);

With, respectively, n = 0,2,4, this yields
c 0 ≈ 0.6366197722,c 2 ≈−0.6870852690,c 4 ≈ 0.05177890435.
If we retain four decimal places, then the sixth partial sum of the Fourier-Legendre expansion of
cos(πx/2) is
2
4
2
cos(πx/2) ≈ 0.6366 − 0.3435(3x − 1) + 0.0065(35x − 30x + 3)
for −1 < x < 1.
Figure 15.4 shows a graph of cos(πx/2) and this partial sum on an interval slightly larger
than [−1,1]. Even with this small number of terms, the partial sum is nearly indistinguishable
from the function on [−1,1], within the scale of the graph. Outside [−1,1], the polynomial
approximation rapidly diverges from cos(πx/2). We would not in general expect to obtain this
good an approximation with as few terms of an eigenfunction expansion.

We conclude this section with some additional properties of Legendre polynomials.

15.2.4 Zeros of Legendre Polynomials
If f is a given function, a number x 0 is a zero of f if f (x 0 ) = 0. Not every function has real
zeros. For example, f (x)=1 + x does not. A real-valued function of a single real variable has a
2
2
zero exactly where its graph crosses the horizontal axis, and the graph of y = 1 + x has no such
crossing.
Notice, however, that for (n = 1,2,3,4,5), the graph of P n (x) in Figure 15.3 crosses the
x-axis exactly n times between −1 and 1, suggesting that each of these functions has n zeros
between −1 and 1.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:20 THM/NEIL Page-528 27410_15_ch15_p505-562