Page 642 - Advanced_Engineering_Mathematics o'neil

622 CHAPTER 17 The Heat Equation

Finally we need

2 π 40 π/4 40 1 − cos(nπ/4)
b n = f (ξ)sin(nξ)dξ = sin(nξ)dξ = .
π 0 π 0 π π
With all the components in place, the solution is

2
∞ 2 −4n t
1 −1 + 4n t + e
n+1
u(x,t) = (−1) sin(nx)
8 n 5
n=1
∞
2
40 1 − cos(nπ/4) −4n t
+ sin(nx)e .
π n
n=1
The second term on the right is the solution of the problem with the xt term omitted. Denote this
“no-source” solution as
∞
40 1 − cos(nπ/4)
2
u 0 (x,t) = sin(nx)e −4n t .
π n
n=1
Then the solution with the source term is

2
∞ 2 −4n t
1 −1 + 4n t + e

u(x,t) = u 0 (x,t) + (−1) n+1 sin(nx).
8 n 5
n=1
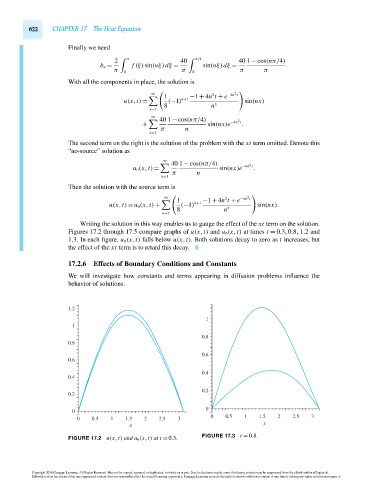
Writing the solution in this way enables us to gauge the effect of the xt term on the solution.
Figures 17.2 through 17.5 compare graphs of u(x,t) and u 0 (x,t) at times t = 0.3,0.8, 1.2 and
1.3. In each figure, u 0 (x,t) falls below u(x,t). Both solutions decay to zero as t increases, but
the effect of the xt term is to retard this decay.
17.2.6 Effects of Boundary Conditions and Constants
We will investigate how constants and terms appearing in diffusion problems influence the
behavior of solutions.

1.2
1
1
0.8
0.8

0.6
0.6
0.4
0.4
0.2
0.2

0
0
0 0.5 1 1.5 2 2.5 3
0 0.5 1 1.5 2 2.5 3
x
x
FIGURE 17.3 t = 0.8.
FIGURE 17.2 u(x,t) and u 0 (x,t) at t = 0.3.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:25 THM/NEIL Page-622 27410_17_ch17_p611-640